Mathematics
From Wikipedia, the free encyclopedia
"Maths" and "Math" redirect here. For other uses see Mathematics (disambiguation) and Math (disambiguation).
Mathematics (from Greek μάθημα máthēma "knowledge, study, learning") is the study of quantity, space, structure, andchange.[2][3] Mathematicians seek out patterns[4][5] and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proof. The research required to solve mathematical problems can take years or even centuries of sustained inquiry. Since the pioneering work of Giuseppe Peano (1858-1932), David Hilbert (1862-1943), and others on axiomatic systems in the late 19th century, it has become customary to view mathematical research as establishing truth byrigorous deduction from appropriately chosen axioms and definitions. When those mathematical structures are good models of real phenomena, then mathematical reasoning often provides insight or predictions.
Through the use of abstraction and logical reasoning, mathematics developed from counting, calculation, measurement, and the systematic study of the shapes and motions of physical objects. Practical mathematics has been a human activity for as far back as written records exist. Rigorous arguments first appeared in Greek mathematics, most notably in Euclid's Elements. Mathematics developed at a relatively slow pace until the Renaissance, when mathematical innovations interacting with newscientific discoveries led to a rapid increase in the rate of mathematical discovery that continues to the present day.[6]
Galileo Galilei (1564-1642) said, 'The universe cannot be read until we have learned the language and become familiar with the characters in which it is written. It is written in mathematical language, and the letters are triangles, circles and other geometrical figures, without which means it is humanly impossible to comprehend a single word. Without these, one is wandering about in a dark labyrinth'.[7] Carl Friedrich Gauss (1777–1855) referred to mathematics as "the Queen of the Sciences".[8] Benjamin Peirce (1809-1880) called mathematics "the science that draws necessary conclusions".[9] David Hilbert said of mathematics: "We are not speaking here of arbitrariness in any sense. Mathematics is not like a game whose tasks are determined by arbitrarily stipulated rules. Rather, it is a conceptual system possessing internal necessity that can only be so and by no means otherwise."[10] Albert Einstein (1879-1955) stated that "as far as the laws of mathematics refer to reality, they are not certain; and as far as they are certain, they do not refer to reality".[11]
Mathematics is used throughout the world as an essential tool in many fields, including natural science, engineering, medicine, and the social sciences. Applied mathematics, the branch of mathematics concerned with application of mathematical knowledge to other fields, inspires and makes use of new mathematical discoveries and sometimes leads to the development of entirely new mathematical disciplines, such as statistics and game theory. Mathematicians also engage in pure mathematics, or mathematics for its own sake, without having any application in mind. There is no clear line separating pure and applied mathematics, and practical applications for what began as pure mathematics are often discovered.[12]
Contents[hide] |
Etymology
The word "mathematics" comes from the Greek μάθημα (máthēma), which means in ancient Greek what one learns, what one gets to know, hence also study and science, and in modern Greek just lesson.
The word máthēma comes from μανθάνω (manthano) in ancient Greek and from μαθαίνω (mathaino) in modern Greek, both of which mean to learn.
The word "mathematics" in Greek came to have the narrower and more technical meaning "mathematical study", even in Classical times.[13] Its adjective is μαθηματικός(mathēmatikós), meaning related to learning or studious, which likewise further came to mean mathematical. In particular, μαθηματικὴ τέχνη (mathēmatikḗ tékhnē), Latin: ars mathematica, meant the mathematical art. In Latin, and in English until around 1700, the term "mathematics" more commonly meant "astrology" (or sometimes "astronomy") rather than "mathematics"; the meaning gradually changed to its present one from about 1500 to 1800. This has resulted in several mistranslations: a particularly notorious one is Saint Augustine's warning that Christians should beware of "mathematici" meaning astrologers, which is sometimes mistranslated as a condemnation of mathematicians.
The apparent plural form in English, like the French plural form les mathématiques (and the less commonly used singular derivative la mathématique), goes back to the Latin neuter plural mathematica (Cicero), based on the Greek plural τα μαθηματικά (ta mathēmatiká), used by Aristotle (384-322BC), and meaning roughly "all things mathematical"; although it is plausible that English borrowed only the adjective mathematic(al) and formed the noun mathematics anew, after the pattern of physics andmetaphysics, which were inherited from the Greek.[14] In English, the noun mathematics takes singular verb forms. It is often shortened to maths or, in English-speaking North America, math.
History
Main article: History of mathematics
The evolution of mathematics might be seen as an ever-increasing series of abstractions, or alternatively an expansion of subject matter. The first abstraction, which is shared by many animals,[15] was probably that of numbers: the realization that a collection of two apples and a collection of two oranges (for example) have something in common, namely quantity of their members.
In addition to recognizing how to count physical objects, prehistoric peoples also recognized how to count abstract quantities, like time – days, seasons, years.[16] Elementary arithmetic (addition, subtraction, multiplication and division) naturally followed.
Since numeracy pre-dated writing, further steps were needed for recording numbers such as tallies or the knotted strings called quipuused by the Inca to store numerical data.[citation needed] Numeral systems have been many and diverse, with the first known written numerals created by Egyptians in Middle Kingdom texts such as the Rhind Mathematical Papyrus.[citation needed]
The earliest uses of mathematics were in trading, land measurement, painting and weavingpatterns and the recording of time. More complex mathematics did not appear until around 3000 BC, when the Babylonians and Egyptians began using arithmetic, algebra and geometry for taxation and other financial calculations, for building and construction, and forastronomy.[17] The systematic study of mathematics in its own right began with theAncient Greeks between 600 and 300 BC.[18]
Mathematics has since been greatly extended, and there has been a fruitful interaction between mathematics and science, to the benefit of both. Mathematical discoveries continue to be made today. According to Mikhail B. Sevryuk, in the January 2006 issue of the Bulletin of the American Mathematical Society, "The number of papers and books included in the Mathematical Reviewsdatabase since 1940 (the first year of operation of MR) is now more than 1.9 million, and more than 75 thousand items are added to the database each year. The overwhelming majority of works in this ocean contain new mathematical theorems and their proofs."[19]
Inspiration, pure and applied mathematics, and aesthetics
Main article: Mathematical beauty
Mathematics arises from many different kinds of problems. At first these were found in commerce, land measurement, architecture and later astronomy; nowadays, all sciences suggest problems studied by mathematicians, and many problems arise within mathematics itself. For example, the physicist Richard Feynman invented the path integral formulation of quantum mechanics using a combination of mathematical reasoning and physical insight, and today's string theory, a still-developing scientific theory which attempts to unify the fourfundamental forces of nature, continues to inspire new mathematics.[20] Some mathematics is only relevant in the area that inspired it, and is applied to solve further problems in that area. But often mathematics inspired by one area proves useful in many areas, and joins the general stock of mathematical concepts. A distinction is often made between pure mathematics and applied mathematics. However pure mathematics topics often turn out to have applications, e.g. number theory in cryptography. This remarkable fact that even the "purest" mathematics often turns out to have practical applications is what Eugene Wigner has called "the unreasonable effectiveness of mathematics".[21] As in most areas of study, the explosion of knowledge in the scientific age has led to specialization: there are now hundreds of specialized areas in mathematics and the latest Mathematics Subject Classification runs to 46 pages.[22] Several areas of applied mathematics have merged with related traditions outside of mathematics and become disciplines in their own right, includingstatistics, operations research, and computer science.
For those who are mathematically inclined, there is often a definite aesthetic aspect to much of mathematics. Many mathematicians talk about the elegance of mathematics, its intrinsic aesthetics and inner beauty. Simplicity and generality are valued. There is beauty in a simple and elegant proof, such as Euclid's proof that there are infinitely many prime numbers, and in an elegant numerical method that speeds calculation, such as the fast Fourier transform. G. H. Hardy in A Mathematician's Apology expressed the belief that these aesthetic considerations are, in themselves, sufficient to justify the study of pure mathematics. He identified criteria such as significance, unexpectedness, inevitability, and economy as factors that contribute to a mathematical aesthetic.[23] Mathematicians often strive to find proofs that are particularly elegant, proofs from "The Book" of God according to Paul Erdős.[24][25] The popularity of recreational mathematics is another sign of the pleasure many find in solving mathematical questions.
Notation, language, and rigor
Main article: Mathematical notation
Most of the mathematical notation in use today was not invented until the 16th century.[26] Before that, mathematics was written out in words, a painstaking process that limited mathematical discovery.[27] Euler (1707–1783) was responsible for many of the notations in use today. Modern notation makes mathematics much easier for the professional, but beginners often find it daunting. It is extremely compressed: a few symbols contain a great deal of information. Like musical notation, modern mathematical notation has a strict syntax (which to a limited extent varies from author to author and from discipline to discipline) and encodes information that would be difficult to write in any other way.
Mathematical language can be difficult to understand for beginners. Words such as or and only have more precise meanings than in everyday speech. Moreover, words such as open and field have been given specialized mathematical meanings. Technical terms such as homeomorphism and integrable have precise meanings in mathematics. Additionally, shorthand phrases such as "iff" for "if and only if" belong to mathematical jargon. There is a reason for special notation and technical vocabulary: mathematics requires more precision than everyday speech. Mathematicians refer to this precision of language and logic as "rigor".
Mathematical proof is fundamentally a matter of rigor. Mathematicians want their theorems to follow from axioms by means of systematic reasoning. This is to avoid mistaken "theorems", based on fallible intuitions, of which many instances have occurred in the history of the subject.[28] The level of rigor expected in mathematics has varied over time: the Greeks expected detailed arguments, but at the time ofIsaac Newton the methods employed were less rigorous. Problems inherent in the definitions used by Newton would lead to a resurgence of careful analysis and formal proof in the 19th century. Misunderstanding the rigor is a cause for some of the common misconceptions of mathematics. Today, mathematicians continue to argue among themselves about computer-assisted proofs. Since large computations are hard to verify, such proofs may not be sufficiently rigorous.[29]
Axioms in traditional thought were "self-evident truths", but that conception is problematic. At a formal level, an axiom is just a string of symbols, which has an intrinsic meaning only in the context of all derivable formulas of an axiomatic system. It was the goal of Hilbert's program to put all of mathematics on a firm axiomatic basis, but according to Gödel's incompleteness theorem every (sufficiently powerful) axiomatic system has undecidable formulas; and so a final axiomatization of mathematics is impossible. Nonetheless mathematics is often imagined to be (as far as its formal content) nothing but set theory in some axiomatization, in the sense that every mathematical statement or proof could be cast into formulas within set theory.[30]
Fields of mathematics
See also: Areas of mathematics
See also: Glossary of areas of mathematics
Mathematics can, broadly speaking, be subdivided into the study of quantity, structure, space, and change (i.e. arithmetic,algebra, geometry, and analysis). In addition to these main concerns, there are also subdivisions dedicated to exploring links from the heart of mathematics to other fields: to logic, to set theory (foundations), to the empirical mathematics of the various sciences (applied mathematics), and more recently to the rigorous study of uncertainty.
Foundations and philosophy
In order to clarify the foundations of mathematics, the fields of mathematical logic and set theory were developed. Mathematical logic includes the mathematical study of logic and the applications of formal logic to other areas of mathematics; set theory is the branch of mathematics that studies sets or collections of objects. Category theory, which deals in an abstract way with mathematical structures and relationships between them, is still in development. The phrase "crisis of foundations" describes the search for a rigorous foundation for mathematics that took place from approximately 1900 to 1930.[31] Some disagreement about the foundations of mathematics continues to the present day. The crisis of foundations was stimulated by a number of controversies at the time, including the controversy over Cantor's set theory and the Brouwer-Hilbert controversy.
Mathematical logic is concerned with setting mathematics within a rigorous axiomatic framework, and studying the implications of such a framework. As such, it is home toGödel's incompleteness theorems which (informally) imply that any formal system that contains basic arithmetic, if sound (meaning that all theorems that can be proven are true), is necessarily incomplete (meaning that there are true theorems which cannot be proved in that system). Whatever finite collection of number-theoretical axioms is taken as a foundation, Gödel showed how to construct a formal statement that is a true number-theoretical fact, but which does not follow from those axioms. Therefore no formal system is a complete axiomatization of full number theory. Modern logic is divided into recursion theory, model theory, and proof theory, and is closely linked totheoretical computer science[citation needed], as well as to Category Theory.
Theoretical computer science includes computability theory, computational complexity theory, and information theory. Computability theory examines the limitations of various theoretical models of the computer, including the most well known model – the Turing machine. Complexity theory is the study of tractability by computer; some problems, although theoretically solvable by computer, are so expensive in terms of time or space that solving them is likely to remain practically unfeasible, even with rapid advance of computer hardware. A famous problem is the "P=NP?" problem, one of the Millennium Prize Problems.[32] Finally, information theory is concerned with the amount of data that can be stored on a given medium, and hence deals with concepts such as compression and entropy.
Pure mathematics
Quantity
The study of quantity starts with numbers, first the familiar natural numbers and integers ("whole numbers") and arithmetical operations on them, which are characterized inarithmetic. The deeper properties of integers are studied in number theory, from which come such popular results as Fermat's Last Theorem. The twin prime conjecture andGoldbach's conjecture are two unsolved problems in number theory.
As the number system is further developed, the integers are recognized as a subset of the rational numbers ("fractions"). These, in turn, are contained within the real numbers, which are used to represent continuous quantities. Real numbers are generalized to complex numbers. These are the first steps of a hierarchy of numbers that goes on to include quarternions and octonions. Consideration of the natural numbers also leads to the transfinite numbers, which formalize the concept of "infinity". Another area of study is size, which leads to the cardinal numbers and then to another conception of infinity: the aleph numbers, which allow meaningful comparison of the size of infinitely large sets.
Structure
Many mathematical objects, such as sets of numbers and functions, exhibit internal structure as a consequence of operations or relations that are defined on the set. Mathematics then studies properties of those sets that can be expressed in terms of that structure; for instance number theory studies properties of the set of integers that can be expressed in terms of arithmetic operations. Moreover, it frequently happens that different such structured sets (or structures) exhibit similar properties, which makes it possible, by a further step of abstraction, to state axioms for a class of structures, and then study at once the whole class of structures satisfying these axioms. Thus one can study groups, rings, fields and other abstract systems; together such studies (for structures defined by algebraic operations) constitute the domain of abstract algebra. By its great generality, abstract algebra can often be applied to seemingly unrelated problems; for instance a number of ancient problems concerning compass and straightedge constructions were finally solved using Galois theory, which involves field theory and group theory. Another example of an algebraic theory is linear algebra, which is the general study of vector spaces, whose elements called vectors have both quantity and direction, and can be used to model (relations between) points in space. This is one example of the phenomenon that the originally unrelated areas of geometry and algebra have very strong interactions in modern mathematics. Combinatoricsstudies ways of enumerating the number of objects that fit a given structure.
Space
The study of space originates with geometry – in particular, Euclidean geometry. Trigonometry is the branch of mathematics that deals with relationships between the sides and the angles of triangles and with the trigonometric functions; it combines space and numbers, and encompasses the well-known Pythagorean theorem. The modern study of space generalizes these ideas to include higher-dimensional geometry, non-Euclidean geometries (which play a central role in general relativity) and topology. Quantity and space both play a role in analytic geometry, differential geometry, and algebraic geometry. Convex and discrete geometry was developed to solve problems innumber theory and functional analysis but now is pursued with an eye on applications in optimization and computer science. Within differential geometry are the concepts offiber bundles and calculus on manifolds, in particular, vector and tensor calculus. Within algebraic geometry is the description of geometric objects as solution sets ofpolynomial equations, combining the concepts of quantity and space, and also the study of topological groups, which combine structure and space. Lie groups are used to study space, structure, and change. Topology in all its many ramifications may have been the greatest growth area in 20th century mathematics; it includes point-set topology, set-theoretic topology, algebraic topology and differential topology. In particular, instances of modern day topology are metrizability theory, axiomatic set theory,homotopy theory, and Morse theory. Topology also includes the now solved Poincaré conjecture. Other results in geometry and topology, including the four color theorem andKepler conjecture, have been proved only with the help of computers.
Change
Understanding and describing change is a common theme in the natural sciences, and calculus was developed as a powerful tool to investigate it. Functions arise here, as a central concept describing a changing quantity. The rigorous study of real numbers and functions of a real variable is known as real analysis, with complex analysis the equivalent field for the complex numbers. Functional analysis focuses attention on (typically infinite-dimensional) spaces of functions. One of many applications of functional analysis is quantum mechanics. Many problems lead naturally to relationships between a quantity and its rate of change, and these are studied as differential equations. Many phenomena in nature can be described by dynamical systems; chaos theory makes precise the ways in which many of these systems exhibit unpredictable yet stilldeterministic behavior.
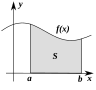 |  |  |  |  |  |
| Calculus | Vector calculus | Differential equations | Dynamical systems | Chaos theory | Complex analysis |
Applied mathematics
Applied mathematics concerns itself with mathematical methods that are typically used in science, engineering, business, and industry. Thus, "applied mathematics" is amathematical science with specialized knowledge. The term "applied mathematics" also describes the professional specialty in which mathematicians work on practical problems; as a profession focused on practical problems, applied mathematics focuses on the formulation, study, and use of mathematical models in science, engineering, and other areas of mathematical practice.
In the past, practical applications have motivated the development of mathematical theories, which then became the subject of study in pure mathematics, where mathematics is developed primarily for its own sake. Thus, the activity of applied mathematics is vitally connected with research in pure mathematics.
Statistics and other decision sciences
Applied mathematics has significant overlap with the discipline of statistics, whose theory is formulated mathematically, especially with probability theory. Statisticians (working as part of a research project) "create data that makes sense" with random sampling and with randomized experiments;[33] the design of a statistical sample or experiment specifies the analysis of the data (before the data be available). When reconsidering data from experiments and samples or when analyzing data fromobservational studies, statisticians "make sense of the data" using the art of modelling and the theory of inference – with model selection and estimation; the estimated models and consequential predictions should be tested on new data.[34]
Statistical theory studies decision problems such as minimizing the risk (expected loss) of a statistical action, such as using a procedure in, for example, parameter estimation, hypothesis testing, and selecting the best. In these traditional areas of mathematical statistics, a statistical-decision problem is formulated by minimizing anobjective function, like expected loss or cost, under specific constraints: For example, a designing a survey often involves minimizing the cost of estimating a population mean with a given level of confidence.[35] Because of its use of optimization, the mathematical theory of statistics shares concerns with other decision sciences, such asoperations research, control theory, and mathematical economics.[36]
Computational mathematics
Computational mathematics proposes and studies methods for solving mathematical problems that are typically too large for human numerical capacity. Numerical analysisstudies methods for problems in analysis using functional analysis and approximation theory; numerical analysis includes the study of approximation and discretizationbroadly with special concern for rounding errors. Numerical analysis and, more broadly, scientific computing also study non-analytic topics of mathematical science, especially algorithmic matrix and graph theory. Other areas of computational mathematics include computer algebra and symbolic computation.
Mathematics as profession
Arguably the most prestigious award in mathematics is the Fields Medal,[37][38] established in 1936 and now awarded every 4 years. The Fields Medal is often considered a mathematical equivalent to the Nobel Prize.
The Wolf Prize in Mathematics, instituted in 1978, recognizes lifetime achievement, and another major international award, the Abel Prize, was introduced in 2003. The Chern Medal was introduced in 2010 to recognize lifetime achievement. These accolades are awarded in recognition of a particular body of work, which may be innovational, or provide a solution to an outstanding problem in an established field.
A famous list of 23 open problems, called "Hilbert's problems", was compiled in 1900 by German mathematician David Hilbert. This list achieved great celebrity among mathematicians, and at least nine of the problems have now been solved. A new list of seven important problems, titled the "Millennium Prize Problems", was published in 2000. Solution of each of these problems carries a $1 million reward, and only one (the Riemann hypothesis) is duplicated in Hilbert's problems.
Mathematics as science
Gauss referred to mathematics as "the Queen of the Sciences".[40] In the original Latin Regina Scientiarum, as well as in GermanKönigin der Wissenschaften, the word corresponding to science means a "field of knowledge", and this was the original meaning of "science" in English, also. Of course, mathematics is in this sense a field of knowledge. The specialization restricting the meaning of "science" to natural science follows the rise of Baconian science, which contrasted "natural science" to scholasticism, the Aristotelean method of inquiring from first principles. Of course, the role of empirical experimentation and observation is negligible in mathematics, compared to natural sciences such as psychology, biology, or physics. Albert Einstein stated that "as far as the laws of mathematics refer to reality, they are not certain; and as far as they are certain, they do not refer to reality."[11] More recently, Marcus du Sautoy has called mathematics 'the Queen of Science...the main driving force behind scientific discovery'.[41]
Many philosophers believe that mathematics is not experimentally falsifiable, and thus not a science according to the definition of Karl Popper.[42] However, in the 1930s Gödel's incompleteness theorems convinced many mathematicians[who?] that mathematics cannot be reduced to logic alone, and Karl Popper concluded that "most mathematical theories are, like those of physics and biology,hypothetico-deductive: pure mathematics therefore turns out to be much closer to the natural sciences whose hypotheses are conjectures, than it seemed even recently."[43] Other thinkers, notably Imre Lakatos, have applied a version of falsificationism to mathematics itself.
An alternative view is that certain scientific fields (such as theoretical physics) are mathematics with axioms that are intended to correspond to reality. In fact, the theoretical physicist, J. M. Ziman, proposed that science is public knowledge and thus includes mathematics.[44] In any case, mathematics shares much in common with many fields in the physical sciences, notably the exploration of the logical consequences of assumptions. Intuition and experimentation also play a role in the formulation of conjectures in both mathematics and the (other) sciences. Experimental mathematicscontinues to grow in importance within mathematics, and computation and simulation are playing an increasing role in both the sciences and mathematics, weakening the objection that mathematics does not use the scientific method.[citation needed]
The opinions of mathematicians on this matter are varied. Many mathematicians[who?] feel that to call their area a science is to downplay the importance of its aesthetic side, and its history in the traditional seven liberal arts; others[who?] feel that to ignore its connection to the sciences is to turn a blind eye to the fact that the interface between mathematics and its applications in science and engineering has driven much development in mathematics. One way this difference of viewpoint plays out is in the philosophical debate as to whether mathematics is created (as in art) or discovered (as in science). It is common to see universities divided into sections that include a division of Science and Mathematics, indicating that the fields are seen as being allied but that they do not coincide. In practice, mathematicians are typically grouped with scientists at the gross level but separated at finer levels. This is one of many issues considered in the philosophy of mathematics.[citation needed]
10 Pythagoras of Samos

Greek Mathematician Pythagoras is considered by some to be one of the first great mathematicians. Living around 570 to 495 BC, in modern day Greece, he is known to have founded the Pythagorean cult, who were noted by Aristotle to be one of the first groups to actively study and advance mathematics. He is also commonly credited with the Pythagorean Theorem within trigonometry. However, some sources doubt that is was him who constructed the proof (Some attribute it to his students, or Baudhayana, who lived some 300 years earlier in India). Nonetheless, the effect of such, as with large portions of fundamental mathematics, is commonly felt today, with the theorem playing a large part in modern measurements and technological equipment, as well as being the base of a large portion of other areas and theorems in mathematics. But, unlike most ancient theories, it played a bearing on the development of geometry, as well as opening the door to the study of mathematics as a worthwhile endeavor. Thus, he could be called the founding father of modern mathematics.
Andrew Wiles

The only currently living mathematician on this list, Andrew Wiles is most well known for his proof of Fermat’s Last Theorem: That no positive integers, a, b and c can satisfy the equation a^n+b^n=c^n For n greater then 2. (If n=2 it is the Pythagoras Formula). Although the contributions to math are not, perhaps, as grand as other on this list, he did ‘invent’ large portions of new mathematics for his proof of the theorem. Besides, his dedication is often admired by most, as he quite literally shut himself away for 7 years to formulate a solution. When it was found that the solution contained an error, he returned to solitude for a further year before the solution was accepted. To put in perspective how ground breaking and new the math was, it had been said that you could count the number of mathematicians in the world on one hand who, at the time, could understand and validate his proof. Nonetheless, the effects of such are likely to only increase as time passes (and more and more people can understand it).
Isaac Newton and Wilhelm Leibniz

I have placed these two together as they are both often given the honor of being the ‘inventor’ of modern infinitesimal calculus, and as such have both made monolithic contributions to the field. To start, Leibniz is often given the credit for introducing modern standard notation, notably the integral sign. He made large contributions to the field of Topology. Whereas all round genius Isaac Newton has, because of the grand scientific epic Principia, generally become the primary man hailed by most to be the actual inventor of calculus. Nonetheless, what can be said is that both men made considerable vast contributions in their own manner.
Leonardo Pisano Blgollo

Blgollo, also known as Leonardo Fibonacci, is perhaps one of the middle ages greatest mathematicians. Living from 1170 to 1250, he is best known for introducing the infamous Fibonacci Series to the western world. Although known to Indian mathematicians since approximately 200 BC, it was, nonetheless, a truly insightful sequence, appearing in biological systems frequently. In addition, from this Fibonacci also contributed greatly to the introduction of the Arabic numbering system. Something he is often forgotten for.
Haven spent a large portion of his childhood within North Africa he learned the Arabic numbering system, and upon realizing it was far simpler and more efficient then the bulky Roman numerals, decided to travel the Arab world learning from the leading mathematicians of the day. Upon returning to Italy in 1202, he published his Liber Abaci, whereupon the Arabic numbers were introduced and applied to many world situations to further advocate their use. As a result of his work the system was gradually adopted and today he is considered a major player in the development of modern mathematics.
Alan Turing

Computer Scientist and Cryptanalyst Alan Turing is regarded my many, if not most, to be one of the greatest minds of the 20th Century. Having worked in the Government Code and Cypher School in Britain during the second world war, he made significant discoveries and created ground breaking methods of code breaking that would eventually aid in cracking the German Enigma Encryptions. Undoubtedly affecting the outcome of the war, or at least the time-scale.
After the end of the war he invested his time in computing. Having come up with idea of a computing style machine before the war, he is considered one of the first true computer scientists. Furthermore, he wrote a range of brilliant papers on the subject of computing that are still relevant today, notably on Artificial Intelligence, on which he developed the Turing test which is still used to evaluate a computers ‘intelligence’. Remarkably, he began in 1948 working with D. G. Champernowne, an undergraduate acquaintance on a computer chess program for a machine not yet in existence. He would play the ‘part’ of the machine in testing such programs.
5René Descartes

French Philosopher, Physicist and Mathematician Rene Descartes is best known for his ‘Cogito Ergo Sum’ philosophy. Despite this, the Frenchman, who lived 1596 to 1650, made ground breaking contributions to mathematics. Alongside Newton and Leibniz, Descartes helped provide the foundations of modern calculus (which Newton and Leibniz later built upon), which in itself had great bearing on the modern day field. Alongside this, and perhaps more familiar to the reader, is his development of Cartesian Geometry, known to most as the standard graph (Square grid lines, x and y axis, etc.) and its use of algebra to describe the various locations on such. Before this most geometers used plain paper (or another material or surface) to preform their art. Previously, such distances had to be measured literally, or scaled. With the introduction of Cartesian Geometry this changed dramatically, points could now be expressed as points on a graph, and as such, graphs could be drawn to any scale, also these points did not necessarily have to be numbers. The final contribution to the field was his introduction of superscripts within algebra to express powers. And thus, like many others in this list, contributed to the development of modern mathematical notation.
Euclid

Living around 300BC, he is considered the Father of Geometry and his magnum opus: Elements, is one the greatest mathematical works in history, with its being in use in education up until the 20th century. Unfortunately, very little is known about his life, and what exists was written long after his presumed death. Nonetheless, Euclid is credited with the instruction of the rigorous, logical proof for theorems and conjectures. Such a framework is still used to this day, and thus, arguably, he has had the greatest influence of all mathematicians on this list. Alongside his Elements were five other surviving works, thought to have been written by him, all generally on the topic of Geometry or Number theory. There are also another five works that have, sadly, been lost throughout history.
G. F. Bernhard Riemann

Bernhard Riemann, born to a poor family in 1826, would rise to become one of the worlds prominent mathematicians in the 19th Century. The list of contributions to geometry are large, and he has a wide range of theorems bearing his name. To name just a few: Riemannian Geometry, Riemannian Surfaces and the Riemann Integral. However, he is perhaps most famous (or infamous) for his legendarily difficult Riemann Hypothesis; an extremely complex problem on the matter of the distributions of prime numbers. Largely ignored for the first 50 years following its appearance, due to few other mathematicians actually understanding his work at the time, it has quickly risen to become one of the greatest open questions in modern science, baffling and confounding even the greatest mathematicians. Although progress has been made, its has been incredibly slow. However, a prize of $1 million has been offered from the Clay Maths Institute for a proof, and one would almost undoubtedly receive a Fields medal if under 40 (The Nobel prize of mathematics). The fallout from such a proof is hypothesized to be large: Major encryption systems are thought to be breakable with such a proof, and all that rely on them would collapse. As well as this, a proof of the hypothesis is expected to use ‘new mathematics’. It would seem that, even in death, Riemann’s work may still pave the way for new contributions to the field, just as he did in life.
Carl Friedrich Gauss

Child prodigy Gauss, the ‘Prince of Mathematics’, made his first major discovery whilst still a teenager, and wrote the incredible Disquisitiones Arithmeticae, his magnum opus, by the time he was 21. Many know Gauss for his outstanding mental ability – quoted to have added the numbers 1 to 100 within seconds whilst attending primary school (with the aid of a clever trick). The local Duke, recognizing his talent, sent him to Collegium Carolinum before he left for Gottingen (at the time it was the most prestigious mathematical university in the world, with many of the best attending). After graduating in 1798 (at the age of 22), he began to make several important contributions in major areas of mathematics, most notably number theory (especially on Prime numbers). He went on to prove the fundamental theorem of algebra, and introduced the Gaussian gravitational constant in physics, as well as much more – all this before he was 24! Needless to say, he continued his work up until his death at the age of 77, and had made major advances in the field which have echoed down through time.
Leonhard Euler

If Gauss is the Prince, Euler is the King. Living from 1707 to 1783, he is regarded as the greatest mathematician to have ever walked this planet. It is said that all mathematical formulas are named after the next person after Euler to discover them. In his day he was ground breaking and on par with Einstein in genius. His primary (if that’s possible) contribution to the field is with the introduction of mathematical notation including the concept of a function (and how it is written as f(x)), shorthand trigonometric functions, the ‘e’ for the base of the natural logarithm (The Euler Constant), the Greek letter Sigma for summation and the letter ‘/i’ for imaginary units, as well as the symbol pi for the ratio of a circles circumference to its diameter. All of which play a huge bearing on modern mathematics, from the every day to the incredibly complex.
As well as this, he also solved the Seven Bridges of Koenigsberg problem in graph theory, found the Euler Characteristic for connecting the number of vertices, edges and faces of an object, and (dis)proved many well known theories, too many to list. Furthermore, he continued to develop calculus, topology, number theory, analysis and graph theory as well as much, much more – and ultimately he paved the way for modern mathematics and all its revelations. It is probably no coincidence that industry and technological developments rapidly increased around this time.
-------------------------------------------------------------------------------------
---------------------------------------------------------------
History of Mathematics in India
In early civilizations, the first expression of maths understanding appears in the form of counting systems.Numbers in early societies were typically represented by groups of lines, though later different numbers came to be assigned specific numeral names and symbols (India) or were designated by alphabetic letters (Rome). Although today, we take our decimal system for granted, not all ancient civilizations based their numbers on a ten-base system. In ancient Babylon, a sexagesimal (base 60) system was in use.
Section 1: Zero and the Place-Value Notation
The number zero is the subtle gift of the Hindus of antiquity to mankind. The concept itself was one of the most significant inventions in the ascent of Man for the growth of culture and civilization. To it must be credited the enormous usefulness of its counterpart, the place value system of expressing all numbers with just ten symbols. And to these two concepts we owe all the arithmetic and mathematics based upon them, the great ease which it has lent to all computations for two millenia and the binary system which now lies at the foundation of communicating with computers. Already in the first three centuries A.D.. the Hindu ancients were using a decimal positional system, that is, a system in which numerals in different positions represent different numbers and in which one of the ten symbols used was a fully functional zero. They called it 'Sunya'. The word and its meaning ‘void’ were obviously borrowed from its use in philosophical literature. Though the Babylonians used a special symbol for zero as early as the 3rd century B.C. , they used it only as a place holder; they did not have the concept of zero as an actual value. It appears the Maya civilisation of South America had a zero in the first century A.D. . but they did not use it in a fixed base system. The Greeks were hampered by their use of letters for the numbers. Before zero was invented, the art of reckoning remained an exclusive and highly skilled profession. It was difficult to distinguish, say, 27, 207, 270, 2007, because the latter three were all written 2 7, with a ‘space’ in between. The positional system is not possible in the Roman numeral system which had no expression or symbol for zero. A number, say, 101,000, would have to be written only by 101 consecutive M’s. The Egyptians had no zero and never reached the idea of expressing all numbers with ten digits. The mathematical climate among the Hindus, however, was congenial for the invention of zero and for its use as the null-value in all facets of calculation, due to four factors:
1. A notation for powers of 10 upto the power 17 was already in use even from vedic times. Single words have been used to denote the powers of the number 10. The numbers one, ten, hundred, thousand, ten thousand, … are given by the sequence of words in the list: eka, dasa, Sata, sahasra, ayuta, laksha, prayuta, koTi, arbuda, abja, kharva, nikharva, mahA-padma, Sankha, jaladhi, antya, mahASankha, parArdha. Thus the decimal system was in the culture even in the early part of the first millenium B.C. . The Yajurveda, in its description of rituals and the mantras employed therein, the Mahabharata and the Ramayanaa in their descriptions of statistics and measurements, used all these words, with total abandon.
2. Counting boards with columns representing units and tens were in use from very ancient times. The numberless content of an empty column in course of time was symbolized to be ‘nothing’.
3. The thriving activity in astrology, astronomy, navigation and business during the first few centuries A.D. naturally looked forward to a superior numerical system that lent itself to complicated calculations.
4. Distinct symbols for the numbers 1 to 9 already existed and the counting system used the base 10 in all its secular, religious and ritual activities. Compare this with the Babylonian numeration which had only three figures, one for 1, one for 10, and one for 100, so that a number, say, 999, would require 27 symbols, namely, nine of each of the symbols.
Of these, the first and fourth factors are probably unique to Hindu culture and contributed most to the thought process that led to the decimal place value notation as well as zero having a value. When exactly the invention of this most modest of all numerals took place, we do not know. The first time it reached Europe was during the Moorish invasion of Spain around 700 A.D. . Later, when massive Latin translations of books from Baghdad took place around the close of the first millenium A.D. the concept was found in an arithmetic book dated 820 A.D. . by Muhammad Ibn Musa al-Khouarizmi who explained the whole system in great detail. The Arabs themselves had no number system of their own. It was the Hindu system he was explaining. That is why the numerals are called the Indo-Arabic numerals even today. It is however a misnomer to call them so; they are already found on the Rock Edits of Ashoka (256 B.C. .). In spite of its being so crucial to our living, it took centuries for the western world to appreciate and incorporate this most valuable numeral, zero, in their recording of accounts or in scholarly writings. For by the time ‘Zero’ reached the West, the Dark Ages of the western world had begun. There are traces, however, of its knowledge in Spain in the tenth century A.D. . But the final breakthrough of the introduction to the West was by Leonardo of Pisa, through his popular text Liber Abaci, 1202 A.D. ., The first European book (in French) that used the zero appeared in 1275.
How the Sunya of the Hindus became the Zero of the modern world is interesting. The 'Sunya' of Sanskrit became the Arabic ‘sifr’ which means empty space. In medieval Latin it manifested as ‘ciphra’ , then in middle English as ‘siphre’, in English as ‘cypher’ and in American as ‘cipher’. In the middle ages, the word ‘ciphra’ evolved to stand for the whole system. In the wake of this general meaning, the Latin ‘zephirum’ came to be used to denote the Sunya. And that entered English finally as ‘zero’. In medieval Europe some countries banned the positional number system, along with zero, brought by the Arabs whom they considered as heathens. So they took Sunya to be a creation of the devil! As a result ‘ciphra’ came to mean a secret code. From this came ‘deciphering’, the resolution of a code!
Section 2. Vedic Mathematics and arithmetical operations
Vedic Mathematics provides an original and refreshing approach to subjects which are usually dismissed as mechanical and tedious. Bharati Krishna Tirtha who published his reconstruction of Vedic Mathematics in 1965, maintains that there are 16 aphorisms and 13 secondary aphorisms which forms his base of the so-called Vedic Mathematics. Though the origins of Vedic Mathematics have not yet been historically established, if nothing else, it provides tremendous insights into the place-value system of numbers without which it would not work. It is amazing that Vedic Mathematics does not require of cramming of multiplication tables beyond 5 x 5. One can improvise all the necessary multiplication tables for oneself and with the aid of the relevant Vedic formulae get the required products very easily, speedily, and correctly, almost immediately. The formulae can be used to evaluate determinants, solve simultaneous linear equations, evaluate logarithms and exponentials. Vedic Mathematics recognises that any algebraic polynomial may be expressed in terms of a positional notation without specifying the base. The same algorithmic scheme as applied to arithmetical operations will easily apply to algebraic problems. And this brings it to the Modern Algebra of Polynomials. It is difficult, in a historical introduction like this to get into the details of Vedic Mathematics. Suffice it to say that with today's over-dependence on calculators for even simple arithmetical computations, the Vedic methods have great pedagogical value and, through their revival, the skills of mental arithmetic may not be lost for posterity.
Section 3. Geometry of the Sulba Sutras
Hailing from the times of the Vedas, the ritual literature which gave directions for constructing sacrificial fires at different times of the year dealt with the their measurement and construction in a systematic and logical way, thus giving rise to the Sulba Sutras. The construction of altars (vedi) and the location of sacrificial fires had to conform to clearly laid down instructions about their shapes and areas in order that they may be effective instruments of sacrifice. The Sulba Sutras provide such instructions for two types of ritual - one for worship at home and one for communal worship. The instructions were mainly for the benefit of craftsmen laying out and building the altars. Bodhayana, Apastamba and Katyayana who have recorded these Sulbasutras were not only priests in the conventional sense but must have been craftsmen themselves. The earliest of them, The Bodhayana Sutras , in three chapters, (800 - 600 B.C.) contains a general statement of the Pythagorean theorem, an approximation procedure for obtaining the square root of two correct to five decimal places and a number of geometric constructions. These latter include an approximate squaring the circle, and construction of rectilinear shapes whose area is equal to the sum or difference of areas of other shapes. The Bodhayana version of the Pythagorean theorem sates as follows:
The rope which is stretched across the diagonal of a square
produces an area double the size of the original square.
It is therefore in the fitness of things that the Pythagorean theorem of Mathematics may be renamed as the Bodhayana theorem.! The other sutras are two centuries later but all of them are prior to Panini of the fourth century B.C. The geometry arising from these sutras give several geometric constructions. Some of these are:
1. To merge two equal or unequal squares to obtain a third square.
2. To transform a rectangle into a square of equal area
3. Squaring a circle and circling a square (approximately)
A remarkable achievement was the discovery of a procedure for evaluating square roots to a high degree of approximation. The square root of two is obtained as
1.4142156 …
the true value being 1.414213… . The fact that such procedures were used successfully by the Sulbasutra geometers to operations with other irrational numbers, is clear proof for negating the western-held opinion that the Sulba sutra geometers borrowed their methods from the Babylonians. The latter's calculation of the square root of two is an isolated instance and further they used the sexagesimal notation for numbers. The achievement of geometrical constructs in Indian mathematics reached its peak later when they arrived at the construction of Sriyantra, which is a complicated diagram, consisting of nine interwoven isosceles triangles, four pointing upwards and four pointing downwards. The triangles are arranged in such a way that they produce 43 subsidiary triangles, at the centre of the smallest of which there is a big dot called the bindu. The difficult problem is to construct the diagram in such a way that all the intersections are correct and the vertices of the largest triangles fall on the circumference of the enclosing circle. In all cases the base angles of the largest triangles is about 51.5 degrees. This has connections with the two most famous irrational numbers of Mathematics, namely p and f. The quantity f, called the golden ratio, has remarkable mathematical properties and is almost a semi-mystical number.
Section 4. Jaina contribution to Fundamentals of Numbers
By the time of the Jains, the role of rituals in the development of mathematics declined and mathematics began to be pursued also for its own sake. The Jains had a fascination for large numbers. Their definitions of the various types of infinities they comprehended are sophisticated, though lacking in mathematical precision. But it must be said to their credit that they were the first, in the chronology of scientific thinking, to have recognised that all infinities were not the same or equal. In fact this idea was established in the mathematical world only in the latter half of the nineteenth century when Cantor initiated his theory of sets.
The Jains were also aware of the theory of indices, though they did not have the modern notation or any convenient notation for the same. Calling the successive squares and square roots as the first, the second, etc. they make the following statement: The first square root multiplied by the second square root is the cube of the second square root. In modern notation this is nothing but the identity in the theory of indices:
a1/2 x a1/4 = (a1/4 )3
They have several such rules for working with powers of a number. They also seem to have had an idea of the logarithm of a number though they don't seem to have put them to practical use in calculation. Another favourite topic with them was the study of permutations and combinations. They had also a great interest in sequences and progressions developed out of their philosophical theory of cosmological structures. A Jain canonical text entitled Triloka prajnApati has a very detailed treatment of arithmetic progressions.
Section 5: The Anonymous Bakshali Manuscript
This manuscript was discovered in 1881 A.D. near a village called Bakshali. It is written in an old form of Sanskrit on seventy leaves of birch bark. It is probably a copy of a manuscript composed in the early centuries A.D. It is a handbook of rules and illustrative examples together with solutions, all mainly on arithmetic and algebra. Fractions, Square roots, Profit and Loss, Interest, Rule of Three, Approximation to surds, Simple equations as well as Simultaneous equations, Quadratic equations, Arithmetic and Geometric Progressions -- all these are covered. Very unusually in the entire history of Ancient Indian mathematics, the subject matter is organised in a sequence: first, a rule or a sutra; then a relevant example in word form; the same in notational form; then the solution and finally the demonstration or the proof. Here for the first time in the history of world mathematics, the Rule of Three is stated in its abstract form. It was from here that the rule was taken to Europe by the Arabs and it was then known as the Golden Rule. It became very popular in Europe after the Renaissance. The rule goes as follows:
If p yields f what will i yield?
Here p stands for pramAna, f for phala and i for icchA.
Here p and i are of the same denomination and
f is of a different denomination.
Write p, f, i in that order. Multiply the middle quantity by the last quantity and divide by the first. The result is fi / p.
The first appearance of indeterminate equations is in the Bakshali mss. This marks the beginning of the continued work on indeterminate equations in India. Such an interest, though originally generated from the demands made by astronomical calculations, was also pursued for its own sake, sometimes even for recreational purposes. The ease with which the place value system is worked in the Bakshali mss. suggests that the system predates the mss. by probably a few centuries.
Section 6. Astronomy
The contribution to Astronomy by ancient Indians is so great that it does not befit it to include it as one of the contributions of Indian Mathematics to the rest of the world. It needs a separate forum all for itself. We shall leave it right there except to add a note on the ancient contribution to the problem of telling time at night by a look at the stars on the meridian. This part is usually not emphasized.
The ancients of India have passed on to us 27 mathematical formulae coded in the Sanskrit language, but not very difficult to remember. In fact, very possibly it has mostly come down to us by oral transmission from generation to generation. For instance, the formula
krittikA simhe kAyA
says that if you see the asterism krittikA (Pleides, in modern terminology) on the meridian, that is the time the Leo (= simha) constellation (of the zodiac) has risen above the horizon by an amount indicated by the word: kAyA. This latter word interpreted in katapayA sankhyA, which is the notation used by astronomers, astrologers and mathematicians to represent numbers, means in this context that the amount of Leo above the (Eastern) horizon is 27 minutes of time. From this and the known position of the Sun on the date in question, one mentally calculates the time of night. On November 7 for example, the Sun is in the middle of Scorpio. So if you see krittikA on the meridian it means Leo has risen 27 minutes before and this means the Sun is behind by
93m (remaining portion of simha)
+ 2h (full portion of kanyA)
+ 2h (full portion of tulA)
+ 60m (half portion of vrischika)
that is 6 hours 33 minutes. In other words it is 6h 33m before sunrise. So it is 11-27 P.M.
Suffice it to say these beautiful formulae constitute an intellectual marvel put to the most mundane use. Never perhaps was so much achieved with so little so early in the Ascent of Man. For details on this, see reference no. [10].
Section 7. Classical contribution to Indeterminate Equations and Algebra
The apex of Mathematical achievement of ancient India occurred during the so-called classical period of Indian Mathematics. The great names are: Aryabhata I (b.476 A.D.) ; Brahmagupta (b.598 A.D.); Bhaskara I (circa 620 A.D.) ; Mahavira (circa 850 A.D.); Sridhara (circa 900 A.D.) ; Bhaskara II (b.1114 A.D.); Nilakantha Somayaji (1445 - 1545 A.D.).
Aryabhata wrote the famous Aryabhatiyam which is an exhaustive exposition of Astronomy. In addition he gave a unique method of representing large numbers by word forms . He systematized all the knowledge of astronomy and mathematics prior to him. The first one in Indian mathematics to give the formula for the area of a triangle was Aryabhata. Several results on Triangles and circles and on Progressions, algorithm for finding cube roots, approximation of p, all these give him a unique position in the development of mathematics. Aryabhata ushered in a Renaissance in Indian Mathematics and Astronomy, that resulted in a remarkable flourishing of science and technology in India. Aryabhata, for the first time, secularised mathematics and astronomy in India and established these as intellectual disciplines in their own right. Excellent commentators followed Aryabhata and to them are due several modifications and applications, explanation of subtle points, and finally, the proofs of results embodied in the sutras of the Master.
Bhaskara I takes a large share of the credit of explaining the too brief and aphoristic statements of Aryabhata. On the important topic of indeterminate equations the Kuttaka method was introduced by Aryabhata and elucidated by Bhaskara I.
Brahmagupta is generally known as the Indian mathematician par excellence. His monumental work Brahma SiddhAnta has 24 chapters of which the latter 14 contain original results on arithmetic algebra and on astronomical instruments. The 12th chapter is on mensuration. The 18th chapter is on Kuttaka. Among his famous results are those on rational right-angled triangles, and cyclic quadrilaterals. He is the earliest one, in the history of world mathematics, to have discussed cyclic quadrilaterals. There is every reason for us to name cyclic quadrilaterals as Brahmagupta Quadrilaterals. It was partly through a translation of Brahma-siddhAnta that the Arabs became aware of Indian astronomy and mathematics.
Bhaskara II's famous work SiddhAnta Siromani has four parts of which the first two are Mathematics and the latter two are astronomy. The first part, LilAvati is an extremely popular text dealing with arithmetic, algebra, geometry and mensuration. The second part, BIjaganitam is a treatise on Advanced Algebra. It contains problems on determining unknown quantities, evaluating surds and solving simple and quadratic equations.
The sheer ingenuity and versatility of Brahmagupta's approach to indeterminate equations of the second degree of the form
N x2 + 1 = y2
is the climax of Indian work in this area. Bhaskara II's cakravAla method to solve such equations is world-famous. By using this powerful method he solved, as one example, the above equation with N = 61 and gave the least integral solution as
x = 226153980 and y = 1766319049.
The famous French mathematician, Fermat, in 1657 A.D. proposed this equation with N = 61 for solution as a challenge to his contemporaries. None of them succeeded in solving the equation in integers. It was not until 1767 A.D. that the western world through Euler, by Lagrange's method of continued fractions, had a complete solution to such types of equations, wrongly called Pell's equation by Euler. But the very same equation, though coincidentally, was completely solved by Bhaskara II five hundred years earlier.
The problem of determining integer solutions of such equations is called Diophantine Analysis after the Greek Mathematician Diophantus (3rd cen. A.D.). As soon as one finds a non-trivial solution (that is, other than the obvious solution x = 0, y = 1) an infinite number of new solutions can be found by repeated application of the Principle of Compositions, known as Brahmagupta's Bhavana Principle. It is Bhaskara's cakravAla method that makes the decisive step in determining a non-trivial solution. Under these circumstances it is appropriate to designate these equations as the Brahmagupta-Bhaskara equations.
Before we leave this topic it is important to mention Srinivasa Ramanujan, the 20th century genius, who revelled in such problems - namely, to determine the possible cases in which a number can be broken up into two or more equal sums of like or unlike powers or more generally to solve intermediate problems in rational numbers.
Bhaskara II introduces also the notion of instantaneous motion of planets. He clearly distinguishes between sthUla gati (average velocity) and sUkshma gati (accurate velocity) in terms of differentials. He also gave formulae for the surface area of a sphere and its volume, and volume of the frustum of a pyramid. Suffice it to say that his work on fundamental operations, his rules of three, five, seven, nine and eleven, his work on permutations and combinations and his handling of zero all speak of a maturity, a culmination of five hundred years of mathematical progress.
Section 8. Indian Trigonometry
Though Trigonometry goes back to the Greek period, the character of the subject started to resemble modern form only after the time of Aryabhata. From here it went to Europe through the Arabs and went into several modifications to reach its present form. In ancient times Trigonometry was considered a part of astronomy. Three functions were introduced: jya, kojya and ukramajya. The first one is r sina where r is the radius of the circle and a is the angle subtended at the centre. The second one is r cosa and the third one is r (1 - cosa). By taking the radius of the circle to be 1, we get the modern trigonometric functions. Various relationships between the sine of an arc and its integral and fractional multiples were used to construct sine tables for different arcs lying between 0 and 90°.
Section 9: Kerala contribution to Infinite Series and Calculus.
Kerala mathematicians produced rules for second order interpolation to calculate intermediate sine values. The Kerala mathematician Madhava may have discovered the sine and cosine series about three hundred years before Newton. In this sense we may consider Madhava to have been the founder of mathematical analysis. Madhava (circa 1340 - 1425 A.D. ) was the first to take the decisive step from the finite procedures of ancient Indian mathematics to treat their limit-passage to infinity. His contributions include infinite-series expansions of circular and trigonometric functions and finite-series approximations. His power series for p and for sine and cosine functions is referred to reverentially by later writers. Many later discoveries in European mathematics ( for example, the Gregory series for the inverse tangent) were anticipated by Kerala astronomer-mathematicians. Nilakantha was mainly an astronomer but his Aryabhatiya bhashya and tantra-sangraha contain work on infinite-series expansions, problems of algebra and spherical geometry.
Section 10. Modern Contribution:
Srinivasa Ramanujan onwards
The second decade of the 20th century compulsorily turned the attention of the mathematical world to India and the Number Theory genius, Srinivasa Ramanujan. The ideas and innovative genius of Ramanujan have not been surpassed ever before or even 100 years after him. His birth, his super-activity in Madras and Cambridge, his glorious rise to international fame and unfortunate death - all happened almost in a flash. But ever since, India has remained on the mathematical map of the world more and more prominently. The 20th century saw the growth of Mathematics in India in the same style, though not in the same speed, the western world has been taking the race for the quest of mathematical knowledge. May we hope that the new millenium will see not only further speed in the acquisition and spread of mathematical knowledge by Indian-born mathematicians, but also further depth in the intensity and relevance of that knowledge, true to its traditions which are at least three millenia old .
Section 1: Zero and the Place-Value Notation
The number zero is the subtle gift of the Hindus of antiquity to mankind. The concept itself was one of the most significant inventions in the ascent of Man for the growth of culture and civilization. To it must be credited the enormous usefulness of its counterpart, the place value system of expressing all numbers with just ten symbols. And to these two concepts we owe all the arithmetic and mathematics based upon them, the great ease which it has lent to all computations for two millenia and the binary system which now lies at the foundation of communicating with computers. Already in the first three centuries A.D.. the Hindu ancients were using a decimal positional system, that is, a system in which numerals in different positions represent different numbers and in which one of the ten symbols used was a fully functional zero. They called it 'Sunya'. The word and its meaning ‘void’ were obviously borrowed from its use in philosophical literature. Though the Babylonians used a special symbol for zero as early as the 3rd century B.C. , they used it only as a place holder; they did not have the concept of zero as an actual value. It appears the Maya civilisation of South America had a zero in the first century A.D. . but they did not use it in a fixed base system. The Greeks were hampered by their use of letters for the numbers. Before zero was invented, the art of reckoning remained an exclusive and highly skilled profession. It was difficult to distinguish, say, 27, 207, 270, 2007, because the latter three were all written 2 7, with a ‘space’ in between. The positional system is not possible in the Roman numeral system which had no expression or symbol for zero. A number, say, 101,000, would have to be written only by 101 consecutive M’s. The Egyptians had no zero and never reached the idea of expressing all numbers with ten digits. The mathematical climate among the Hindus, however, was congenial for the invention of zero and for its use as the null-value in all facets of calculation, due to four factors:
1. A notation for powers of 10 upto the power 17 was already in use even from vedic times. Single words have been used to denote the powers of the number 10. The numbers one, ten, hundred, thousand, ten thousand, … are given by the sequence of words in the list: eka, dasa, Sata, sahasra, ayuta, laksha, prayuta, koTi, arbuda, abja, kharva, nikharva, mahA-padma, Sankha, jaladhi, antya, mahASankha, parArdha. Thus the decimal system was in the culture even in the early part of the first millenium B.C. . The Yajurveda, in its description of rituals and the mantras employed therein, the Mahabharata and the Ramayanaa in their descriptions of statistics and measurements, used all these words, with total abandon.
2. Counting boards with columns representing units and tens were in use from very ancient times. The numberless content of an empty column in course of time was symbolized to be ‘nothing’.
3. The thriving activity in astrology, astronomy, navigation and business during the first few centuries A.D. naturally looked forward to a superior numerical system that lent itself to complicated calculations.
4. Distinct symbols for the numbers 1 to 9 already existed and the counting system used the base 10 in all its secular, religious and ritual activities. Compare this with the Babylonian numeration which had only three figures, one for 1, one for 10, and one for 100, so that a number, say, 999, would require 27 symbols, namely, nine of each of the symbols.
Of these, the first and fourth factors are probably unique to Hindu culture and contributed most to the thought process that led to the decimal place value notation as well as zero having a value. When exactly the invention of this most modest of all numerals took place, we do not know. The first time it reached Europe was during the Moorish invasion of Spain around 700 A.D. . Later, when massive Latin translations of books from Baghdad took place around the close of the first millenium A.D. the concept was found in an arithmetic book dated 820 A.D. . by Muhammad Ibn Musa al-Khouarizmi who explained the whole system in great detail. The Arabs themselves had no number system of their own. It was the Hindu system he was explaining. That is why the numerals are called the Indo-Arabic numerals even today. It is however a misnomer to call them so; they are already found on the Rock Edits of Ashoka (256 B.C. .). In spite of its being so crucial to our living, it took centuries for the western world to appreciate and incorporate this most valuable numeral, zero, in their recording of accounts or in scholarly writings. For by the time ‘Zero’ reached the West, the Dark Ages of the western world had begun. There are traces, however, of its knowledge in Spain in the tenth century A.D. . But the final breakthrough of the introduction to the West was by Leonardo of Pisa, through his popular text Liber Abaci, 1202 A.D. ., The first European book (in French) that used the zero appeared in 1275.
How the Sunya of the Hindus became the Zero of the modern world is interesting. The 'Sunya' of Sanskrit became the Arabic ‘sifr’ which means empty space. In medieval Latin it manifested as ‘ciphra’ , then in middle English as ‘siphre’, in English as ‘cypher’ and in American as ‘cipher’. In the middle ages, the word ‘ciphra’ evolved to stand for the whole system. In the wake of this general meaning, the Latin ‘zephirum’ came to be used to denote the Sunya. And that entered English finally as ‘zero’. In medieval Europe some countries banned the positional number system, along with zero, brought by the Arabs whom they considered as heathens. So they took Sunya to be a creation of the devil! As a result ‘ciphra’ came to mean a secret code. From this came ‘deciphering’, the resolution of a code!
Section 2. Vedic Mathematics and arithmetical operations
Vedic Mathematics provides an original and refreshing approach to subjects which are usually dismissed as mechanical and tedious. Bharati Krishna Tirtha who published his reconstruction of Vedic Mathematics in 1965, maintains that there are 16 aphorisms and 13 secondary aphorisms which forms his base of the so-called Vedic Mathematics. Though the origins of Vedic Mathematics have not yet been historically established, if nothing else, it provides tremendous insights into the place-value system of numbers without which it would not work. It is amazing that Vedic Mathematics does not require of cramming of multiplication tables beyond 5 x 5. One can improvise all the necessary multiplication tables for oneself and with the aid of the relevant Vedic formulae get the required products very easily, speedily, and correctly, almost immediately. The formulae can be used to evaluate determinants, solve simultaneous linear equations, evaluate logarithms and exponentials. Vedic Mathematics recognises that any algebraic polynomial may be expressed in terms of a positional notation without specifying the base. The same algorithmic scheme as applied to arithmetical operations will easily apply to algebraic problems. And this brings it to the Modern Algebra of Polynomials. It is difficult, in a historical introduction like this to get into the details of Vedic Mathematics. Suffice it to say that with today's over-dependence on calculators for even simple arithmetical computations, the Vedic methods have great pedagogical value and, through their revival, the skills of mental arithmetic may not be lost for posterity.
Section 3. Geometry of the Sulba Sutras
Hailing from the times of the Vedas, the ritual literature which gave directions for constructing sacrificial fires at different times of the year dealt with the their measurement and construction in a systematic and logical way, thus giving rise to the Sulba Sutras. The construction of altars (vedi) and the location of sacrificial fires had to conform to clearly laid down instructions about their shapes and areas in order that they may be effective instruments of sacrifice. The Sulba Sutras provide such instructions for two types of ritual - one for worship at home and one for communal worship. The instructions were mainly for the benefit of craftsmen laying out and building the altars. Bodhayana, Apastamba and Katyayana who have recorded these Sulbasutras were not only priests in the conventional sense but must have been craftsmen themselves. The earliest of them, The Bodhayana Sutras , in three chapters, (800 - 600 B.C.) contains a general statement of the Pythagorean theorem, an approximation procedure for obtaining the square root of two correct to five decimal places and a number of geometric constructions. These latter include an approximate squaring the circle, and construction of rectilinear shapes whose area is equal to the sum or difference of areas of other shapes. The Bodhayana version of the Pythagorean theorem sates as follows:
The rope which is stretched across the diagonal of a square
produces an area double the size of the original square.
It is therefore in the fitness of things that the Pythagorean theorem of Mathematics may be renamed as the Bodhayana theorem.! The other sutras are two centuries later but all of them are prior to Panini of the fourth century B.C. The geometry arising from these sutras give several geometric constructions. Some of these are:
1. To merge two equal or unequal squares to obtain a third square.
2. To transform a rectangle into a square of equal area
3. Squaring a circle and circling a square (approximately)
A remarkable achievement was the discovery of a procedure for evaluating square roots to a high degree of approximation. The square root of two is obtained as
1.4142156 …
the true value being 1.414213… . The fact that such procedures were used successfully by the Sulbasutra geometers to operations with other irrational numbers, is clear proof for negating the western-held opinion that the Sulba sutra geometers borrowed their methods from the Babylonians. The latter's calculation of the square root of two is an isolated instance and further they used the sexagesimal notation for numbers. The achievement of geometrical constructs in Indian mathematics reached its peak later when they arrived at the construction of Sriyantra, which is a complicated diagram, consisting of nine interwoven isosceles triangles, four pointing upwards and four pointing downwards. The triangles are arranged in such a way that they produce 43 subsidiary triangles, at the centre of the smallest of which there is a big dot called the bindu. The difficult problem is to construct the diagram in such a way that all the intersections are correct and the vertices of the largest triangles fall on the circumference of the enclosing circle. In all cases the base angles of the largest triangles is about 51.5 degrees. This has connections with the two most famous irrational numbers of Mathematics, namely p and f. The quantity f, called the golden ratio, has remarkable mathematical properties and is almost a semi-mystical number.
Section 4. Jaina contribution to Fundamentals of Numbers
By the time of the Jains, the role of rituals in the development of mathematics declined and mathematics began to be pursued also for its own sake. The Jains had a fascination for large numbers. Their definitions of the various types of infinities they comprehended are sophisticated, though lacking in mathematical precision. But it must be said to their credit that they were the first, in the chronology of scientific thinking, to have recognised that all infinities were not the same or equal. In fact this idea was established in the mathematical world only in the latter half of the nineteenth century when Cantor initiated his theory of sets.
The Jains were also aware of the theory of indices, though they did not have the modern notation or any convenient notation for the same. Calling the successive squares and square roots as the first, the second, etc. they make the following statement: The first square root multiplied by the second square root is the cube of the second square root. In modern notation this is nothing but the identity in the theory of indices:
a1/2 x a1/4 = (a1/4 )3
They have several such rules for working with powers of a number. They also seem to have had an idea of the logarithm of a number though they don't seem to have put them to practical use in calculation. Another favourite topic with them was the study of permutations and combinations. They had also a great interest in sequences and progressions developed out of their philosophical theory of cosmological structures. A Jain canonical text entitled Triloka prajnApati has a very detailed treatment of arithmetic progressions.
Section 5: The Anonymous Bakshali Manuscript
This manuscript was discovered in 1881 A.D. near a village called Bakshali. It is written in an old form of Sanskrit on seventy leaves of birch bark. It is probably a copy of a manuscript composed in the early centuries A.D. It is a handbook of rules and illustrative examples together with solutions, all mainly on arithmetic and algebra. Fractions, Square roots, Profit and Loss, Interest, Rule of Three, Approximation to surds, Simple equations as well as Simultaneous equations, Quadratic equations, Arithmetic and Geometric Progressions -- all these are covered. Very unusually in the entire history of Ancient Indian mathematics, the subject matter is organised in a sequence: first, a rule or a sutra; then a relevant example in word form; the same in notational form; then the solution and finally the demonstration or the proof. Here for the first time in the history of world mathematics, the Rule of Three is stated in its abstract form. It was from here that the rule was taken to Europe by the Arabs and it was then known as the Golden Rule. It became very popular in Europe after the Renaissance. The rule goes as follows:
If p yields f what will i yield?
Here p stands for pramAna, f for phala and i for icchA.
Here p and i are of the same denomination and
f is of a different denomination.
Write p, f, i in that order. Multiply the middle quantity by the last quantity and divide by the first. The result is fi / p.
The first appearance of indeterminate equations is in the Bakshali mss. This marks the beginning of the continued work on indeterminate equations in India. Such an interest, though originally generated from the demands made by astronomical calculations, was also pursued for its own sake, sometimes even for recreational purposes. The ease with which the place value system is worked in the Bakshali mss. suggests that the system predates the mss. by probably a few centuries.
Section 6. Astronomy
The contribution to Astronomy by ancient Indians is so great that it does not befit it to include it as one of the contributions of Indian Mathematics to the rest of the world. It needs a separate forum all for itself. We shall leave it right there except to add a note on the ancient contribution to the problem of telling time at night by a look at the stars on the meridian. This part is usually not emphasized.
The ancients of India have passed on to us 27 mathematical formulae coded in the Sanskrit language, but not very difficult to remember. In fact, very possibly it has mostly come down to us by oral transmission from generation to generation. For instance, the formula
krittikA simhe kAyA
says that if you see the asterism krittikA (Pleides, in modern terminology) on the meridian, that is the time the Leo (= simha) constellation (of the zodiac) has risen above the horizon by an amount indicated by the word: kAyA. This latter word interpreted in katapayA sankhyA, which is the notation used by astronomers, astrologers and mathematicians to represent numbers, means in this context that the amount of Leo above the (Eastern) horizon is 27 minutes of time. From this and the known position of the Sun on the date in question, one mentally calculates the time of night. On November 7 for example, the Sun is in the middle of Scorpio. So if you see krittikA on the meridian it means Leo has risen 27 minutes before and this means the Sun is behind by
93m (remaining portion of simha)
+ 2h (full portion of kanyA)
+ 2h (full portion of tulA)
+ 60m (half portion of vrischika)
that is 6 hours 33 minutes. In other words it is 6h 33m before sunrise. So it is 11-27 P.M.
Suffice it to say these beautiful formulae constitute an intellectual marvel put to the most mundane use. Never perhaps was so much achieved with so little so early in the Ascent of Man. For details on this, see reference no. [10].
Section 7. Classical contribution to Indeterminate Equations and Algebra
The apex of Mathematical achievement of ancient India occurred during the so-called classical period of Indian Mathematics. The great names are: Aryabhata I (b.476 A.D.) ; Brahmagupta (b.598 A.D.); Bhaskara I (circa 620 A.D.) ; Mahavira (circa 850 A.D.); Sridhara (circa 900 A.D.) ; Bhaskara II (b.1114 A.D.); Nilakantha Somayaji (1445 - 1545 A.D.).
Aryabhata wrote the famous Aryabhatiyam which is an exhaustive exposition of Astronomy. In addition he gave a unique method of representing large numbers by word forms . He systematized all the knowledge of astronomy and mathematics prior to him. The first one in Indian mathematics to give the formula for the area of a triangle was Aryabhata. Several results on Triangles and circles and on Progressions, algorithm for finding cube roots, approximation of p, all these give him a unique position in the development of mathematics. Aryabhata ushered in a Renaissance in Indian Mathematics and Astronomy, that resulted in a remarkable flourishing of science and technology in India. Aryabhata, for the first time, secularised mathematics and astronomy in India and established these as intellectual disciplines in their own right. Excellent commentators followed Aryabhata and to them are due several modifications and applications, explanation of subtle points, and finally, the proofs of results embodied in the sutras of the Master.
Bhaskara I takes a large share of the credit of explaining the too brief and aphoristic statements of Aryabhata. On the important topic of indeterminate equations the Kuttaka method was introduced by Aryabhata and elucidated by Bhaskara I.
Brahmagupta is generally known as the Indian mathematician par excellence. His monumental work Brahma SiddhAnta has 24 chapters of which the latter 14 contain original results on arithmetic algebra and on astronomical instruments. The 12th chapter is on mensuration. The 18th chapter is on Kuttaka. Among his famous results are those on rational right-angled triangles, and cyclic quadrilaterals. He is the earliest one, in the history of world mathematics, to have discussed cyclic quadrilaterals. There is every reason for us to name cyclic quadrilaterals as Brahmagupta Quadrilaterals. It was partly through a translation of Brahma-siddhAnta that the Arabs became aware of Indian astronomy and mathematics.
Bhaskara II's famous work SiddhAnta Siromani has four parts of which the first two are Mathematics and the latter two are astronomy. The first part, LilAvati is an extremely popular text dealing with arithmetic, algebra, geometry and mensuration. The second part, BIjaganitam is a treatise on Advanced Algebra. It contains problems on determining unknown quantities, evaluating surds and solving simple and quadratic equations.
The sheer ingenuity and versatility of Brahmagupta's approach to indeterminate equations of the second degree of the form
N x2 + 1 = y2
is the climax of Indian work in this area. Bhaskara II's cakravAla method to solve such equations is world-famous. By using this powerful method he solved, as one example, the above equation with N = 61 and gave the least integral solution as
x = 226153980 and y = 1766319049.
The famous French mathematician, Fermat, in 1657 A.D. proposed this equation with N = 61 for solution as a challenge to his contemporaries. None of them succeeded in solving the equation in integers. It was not until 1767 A.D. that the western world through Euler, by Lagrange's method of continued fractions, had a complete solution to such types of equations, wrongly called Pell's equation by Euler. But the very same equation, though coincidentally, was completely solved by Bhaskara II five hundred years earlier.
The problem of determining integer solutions of such equations is called Diophantine Analysis after the Greek Mathematician Diophantus (3rd cen. A.D.). As soon as one finds a non-trivial solution (that is, other than the obvious solution x = 0, y = 1) an infinite number of new solutions can be found by repeated application of the Principle of Compositions, known as Brahmagupta's Bhavana Principle. It is Bhaskara's cakravAla method that makes the decisive step in determining a non-trivial solution. Under these circumstances it is appropriate to designate these equations as the Brahmagupta-Bhaskara equations.
Before we leave this topic it is important to mention Srinivasa Ramanujan, the 20th century genius, who revelled in such problems - namely, to determine the possible cases in which a number can be broken up into two or more equal sums of like or unlike powers or more generally to solve intermediate problems in rational numbers.
Bhaskara II introduces also the notion of instantaneous motion of planets. He clearly distinguishes between sthUla gati (average velocity) and sUkshma gati (accurate velocity) in terms of differentials. He also gave formulae for the surface area of a sphere and its volume, and volume of the frustum of a pyramid. Suffice it to say that his work on fundamental operations, his rules of three, five, seven, nine and eleven, his work on permutations and combinations and his handling of zero all speak of a maturity, a culmination of five hundred years of mathematical progress.
Section 8. Indian Trigonometry
Though Trigonometry goes back to the Greek period, the character of the subject started to resemble modern form only after the time of Aryabhata. From here it went to Europe through the Arabs and went into several modifications to reach its present form. In ancient times Trigonometry was considered a part of astronomy. Three functions were introduced: jya, kojya and ukramajya. The first one is r sina where r is the radius of the circle and a is the angle subtended at the centre. The second one is r cosa and the third one is r (1 - cosa). By taking the radius of the circle to be 1, we get the modern trigonometric functions. Various relationships between the sine of an arc and its integral and fractional multiples were used to construct sine tables for different arcs lying between 0 and 90°.
Section 9: Kerala contribution to Infinite Series and Calculus.
Kerala mathematicians produced rules for second order interpolation to calculate intermediate sine values. The Kerala mathematician Madhava may have discovered the sine and cosine series about three hundred years before Newton. In this sense we may consider Madhava to have been the founder of mathematical analysis. Madhava (circa 1340 - 1425 A.D. ) was the first to take the decisive step from the finite procedures of ancient Indian mathematics to treat their limit-passage to infinity. His contributions include infinite-series expansions of circular and trigonometric functions and finite-series approximations. His power series for p and for sine and cosine functions is referred to reverentially by later writers. Many later discoveries in European mathematics ( for example, the Gregory series for the inverse tangent) were anticipated by Kerala astronomer-mathematicians. Nilakantha was mainly an astronomer but his Aryabhatiya bhashya and tantra-sangraha contain work on infinite-series expansions, problems of algebra and spherical geometry.
Section 10. Modern Contribution:
Srinivasa Ramanujan onwards
The second decade of the 20th century compulsorily turned the attention of the mathematical world to India and the Number Theory genius, Srinivasa Ramanujan. The ideas and innovative genius of Ramanujan have not been surpassed ever before or even 100 years after him. His birth, his super-activity in Madras and Cambridge, his glorious rise to international fame and unfortunate death - all happened almost in a flash. But ever since, India has remained on the mathematical map of the world more and more prominently. The 20th century saw the growth of Mathematics in India in the same style, though not in the same speed, the western world has been taking the race for the quest of mathematical knowledge. May we hope that the new millenium will see not only further speed in the acquisition and spread of mathematical knowledge by Indian-born mathematicians, but also further depth in the intensity and relevance of that knowledge, true to its traditions which are at least three millenia old .
------------------------------------------------------------------------------------
Hi story of MatHeMati cs
The importance of Mathematics in everyday life
MATHS IN EVERYDAY LIFE
FUTURE CARRIERS IN MATHS
Vedic Mathematics
Mutation
What is Mathematics?
-----------------------------------------------------------------------------------------------
What is Math?
math·e·mat·ics n. (used with a sing. verb). The study of the measurement, properties, and relationships of quantities, using numbers and symbols. [From Middle English mathematik, from Old French mathematique, from Latin mathematica, from Greek mathematike (tekhne)]
math-e-mat-ics n. ... the science of numbers and their operations, interrelations, combinations, generalizations, and abstractions and of space configurations and their structure, measurement, transformations, and generalizations.
Webster's New Collegiate DictionaryMathematics is a language.
Gibbs, Josiah Willard. 1839-1903.To those who do not know Mathematics it is difficult to get across a real feeling as to the beauty, the deepest beauty of nature. ... If you want to learn about nature, to appreciate nature, it is necessary to understand the language that she speaks in.
American mathematician and physicist.
Richard Feynman. 1918-1988.
American physicist.
The Character of Physical Law
Mathematics may be defined as the subject in which we never know what we are talking about, nor whether what we are saying is true.
Bertrand Russell. 1872–1970All science requires Mathematics. The knowledge of mathematical things is almost innate in us... This is the easiest of sciences, a fact which is obvious in that no one’s brain rejects it; for laymen and people who are utterly illiterate know how to count and reckon.
British philosopher, mathematician.
Mysticism and Logic
Roger Bacon. 1214-1294
English philosopher, scientist.
Opus MaiusMore quotes on the nature of Mathematics: http://math.furman.edu/cgi-bin/randquote.pl
What is mathematics? Most people would say it has something to do with numbers, but numbers are just one type of mathematical structure. Saying "math is the study of numbers" (or something similar) is like saying that "zoology is the study of giraffes". Math may be better thought of as the study of patterns, but this too falls short...The more I study math, the more I wonder about what exactly math is. Actually nobody knows. It seems to be a product or our minds, and yet reflects the external universe with uncanny accuracy. A mathematician develops a mathematical theory for its aesthetic unworldly beauty and it's compelling evolution, with no thought of how it might be applied to the world. A century later a physicist finds this theory to be perfect to use as a framework to express his physics (this sort of thing happens frequently). Pretty weird how intimately connected our innermost "mind" and the outermost "universe" really are. This is a profound mystery!Bruce Bennett, my advisor in grad school, defines mathematics as "unified consciousness theory". As you come to master a branch of mathematics, it's as though you've grown a new abstract organ of perception through which you may then view the world. You've grown a new "mind's eye" that can perceive realities literally inconceivable without this new organ of perception.Rafael Espericueta
Professor of Mathematics
Bakersfield College
-------------------------------------------------------------------------------------------
IMP site
Famous Indian Mathematicians Biography

The most fundamental contribution of ancient India in mathematics is the invention of decimal system of enumeration, including the invention of zero. The decimal system uses nine digits (1 to 9) and the symbol zero (for nothing) to denote all natural numbers by assigning a place value to the digits. The Arabs carried this system to Africa and Europe.
The Vedas and Valmiki Ramayana used this system, though the exact dates of these works are not known. MohanjoDaro and Harappa excavations (which may be around 3000 B.C. old) also give specimens of writing in India. Aryans came 1000 years later, around 2000 B.C. Being very religious people, they were deeply interested in planetary positions to calculate auspicious times, and they developed astronomy and mathematics towards this end. They identified various nakshatras (constellations) and named the months after them. They could count up to 1012, while the Greeks could count up to 104 and Romans up to 108. Values of irrational numbers such as
In the year 1881 A.D., at a village named Bakhshali near Peshawar, a farmer found a manuscript during excavation. About 70 leaves were found, and are now famous as the Bakhshali Manuscript. Western scholars estimate its date as about third or fourth century A.D. It is devoted mostly to arithmetic and algebra, with a few problems on geometry and mensuration.
With this historical background, we come to the famous Indian mathematicians.
Aryabhata (475 A.D. -550 A.D.) is the first well known Indian mathematician. Born in Kerala, he completed his studies at the university of Nalanda. In the section Ganita (calculations) of his astronomical treatiseAryabhatiya (499 A.D.), he made the fundamental advance in finding the lengths of chords of circles, by using the half chord rather than the full chord method used by Greeks. He gave the value of
Brahmagupta (598 A.D. -665 A.D.) is renowned for introduction of negative numbers and operations on zero into arithmetic. His main work wasBrahmasphutasiddhanta, which was a corrected version of old astronomical treatise Brahmasiddhanta. This work was later translated into Arabic as Sind Hind. He formulated the rule of three and proposed rules for the solution of quadratic and simultaneous equations. He gave the formula for the area of a cyclic quadrilateral as
After Brahmagupta, the mathematician of some consequence was Sridhara, who wrote Patiganita Sara, a book on algebra, in 750 A.D. Even Bhaskara refers to his works. After Sridhara, the most celebrated mathematician was Mahaviracharaya or Mahavira. He wrote Ganita Sara Sangraha in 850 A.D., which is the first text book on arithmetic in present day form. He is the only Indian mathematician who has briefly referred to the ellipse (which he called Ayatvrit). The Greeks, by contrast, had studied conic sections in great detail.
Bhaskara (1114 A.D. -1185 A.D.) or Bhaskaracharaya is the most well known ancient Indian mathematician. He was born in 1114 A.D. at Bijjada Bida (Bijapur, Karnataka) in the Sahyadari Hills. He was the first to declare that any number divided by zero is infinity and that the sum of any number and infinity is also infinity. He is famous for his book Siddhanta Siromani(1150 A.D.). It is divided into four sections -Leelavati (a book on arithmetic),Bijaganita (algebra), Goladhayaya (chapter on sphere -celestial globe), andGrahaganita (mathematics of the planets). Leelavati contains many interesting problems and was a very popular text book. Bhaskara introducedchakrawal, or the cyclic method, to solve algebraic equations. Six centurieslater, European mathematicians like Galois, Euler and Lagrange rediscovered this method and called it "inverse cyclic". Bhaskara can also be called the founder of differential calculus. He gave an example of what is now called "differential coefficient" and the basic idea of what is now called "Rolle's theorem". Unfortunately, later Indian mathematicians did not take any notice of this. Five centuries later, Newton and Leibniz developed this subject. As an astronomer, Bhaskara is renowned for his concept of Tatkalikagati(instantaneous motion).
After this period, India was repeatedly raided by muslims and other rulers and there was a lull in scientific research. Industrial revolution and Renaissance passed India by. Before Ramanujan, the only noteworthy mathematician was Sawai Jai Singh II, who founded the present city of Jaipur in 1727 A.D. This Hindu king was a great patron of mathematicians and astronomers. He is known for building observatories (Jantar Mantar) at Delhi, Jaipur, Ujjain, Varanasi and Mathura. Among the instruments he designed himself are Samrat Yantra, Ram Yantra and Jai Parkash.
Well known Indian mathematicians of 20th century are:
Srinivasa Aaiyangar Ramanujan is undoubtedly the most celebrated Indian Mathematical genius. He was born in a poor family at Erode in Tamil Nadu on December 22, 1887. Largely self taught, he feasted on Loney's Trigonometry at the age of 13, and at the age of 15, his senior friends gave him Synopsis of Elementary Results in Pure and Applied Mathematics by GeorgeCarr. He used to write his ideas and results on loose sheets. His three filled notebooks are now famous as Ramanujan's Frayed Notebooks. Though he had no qualifying degree, the University of Madras granted him a monthly scholarship of Rs. 75 in 1913. A few months earlier, he had sent a letter to great mathematician G.H. Hardy, in which he mentioned 120 theorems and formulae. Hardy and his colleague at Cambridge University, J.E. Littlewood immediately recognised his genius. Ramanujan sailed for Britain on March 17, 1914. Between 1914 and 1917, Ramanujan published 21 papers, some in collaboration with Hardy. His achievements include Hardy-Ramanujan-Littlewood circle method in number theory, Roger-Ramanujan's identities in partition of numbers, work on algebra of inequalities, elliptic functions, continued fractions, partial sums and products of hypergeometric series, etc. He was the second Indian to be elected Fellow of the Royal Society in February, 1918. Later that year, he became the first Indian to be elected Fellow of Trinity College, Cambridge. Ramanujan had an intimate familiarity with numbers. During an illness in England, Hardy visited Ramanujan in the hospital. When Hardy remarked that he had taken taxi number 1729, a singularly unexceptional number, Ramanujan immediately responded that this number was actually quite remarkable: it is the smallest integer that can be represented in two ways by the sum of two cubes: 1729=1³+12³=9³+10³.
Unfortunately, Ramanujan's health deteriorated due to tuberculosis, and he returnted to India in 1919. He died in Madras on April 26, 1920.
P.C. Mahalanobis : He founded the Indian Statistical Research Institute in Calcutta. In 1958, he started the National Sample Surveys which gained international fame. He died in 1972 at the age of 79.
C.R. Rao : A well known statistician, famous for his "theory of estimation"(1945). His formulae and theory include "Cramer -Rao inequality", "Fischer -Rao theorem" and "Rao - Blackwellisation".
D.R. Kaprekar (1905-1988) : Fond of numbers. Well known for "Kaprekar Constant" 6174. Take any four digit number in which all digits are not alike. Arrange its digits in descending order and subtract from it the number formed by arranging the digits in ascending order. If this process is repeated with reminders, ultimately number 6174 is obtained, which then generates itself.
Harish Chandra (1923-1983) : Greatly developed the branch of higher mathematics known as the infinite dimensional group representation theory.
Narendra Karmarkar : India born Narendra Karmarkar, working at Bell Labs USA, stunned the world in 1984 with his new algorithm to solve linear programming problems. This made the complex calculations much faster, and had immediate applications in airports, warehouses, communication networks etc.
 Isaac Newton |  Archimedes |  Carl Gauss |  Leonhard Euler |  Bernhard Riemann |  Euclid |
 Henri Poincaré |  J.-L. Lagrange |  David Hilbert |  G.W. Leibniz |  Alex. Grothendieck |  Pierre de Fermat |


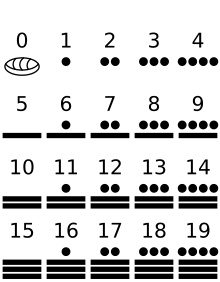



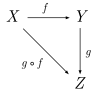










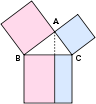











No comments:
Post a Comment