A Brief History of Zero and Indian Numerals

A Brief History of Zero and Indian Numerals

http://arxiv.org/ftp/arxiv/papers/0707/0707.3579.pdf
http://historyofzero.blogspot.com/2008/07/undoubtedly-complete-credit-goes-to.html
http://www.brusselsjournal.com/node/4107
http://www.mediatinker.com/blog/archives/008821.html

http://www.storyofmathematics.com/mathematicians.html

http://www.slideshare.net/rock432/walker-geometry-project

http://www.slideshare.net/dee77/math-powerpoint-for-presentation
http://www.intmath.com/numbers/4-powers-roots-radicals.php
http://www.slideshare.net/lamarquesadelasnavas/artistic-maths-7851281


http://www.ehow.com/about_6530350_importance-math-everyday-life.html


http://www.infoplease.com/ce6/sci/A0859533.html




http://mathandreadinghelp.org/articles/The_importance_of_math_education.html
http://www.mathsinquiry.org.uk/report/chapter-1.html

http://www.rbs0.com/math.htm

Mathematics for Physicists and Electrical Engineers

Copyright 1988 and 2000 by Ronald B. Standler

The following paper was prepared in 1988 when I was an Associate Professor of Electrical Engineering at the main campus of The Pennsylvania State University and a member of the Electrical Engineering Department's Curriculum Committee.

There are two reasons that this paper is posted here on the Internet:

1. Encourage mathematics teachers and professors to concentrate on certain topics, and to include derivations and "word problems" on every examination.
2. Inform pupils and students who are contemplating a career in engineering, chemistry, or physics that mathematics is not only important, it is essential to the practice of those professions.

cite as: Ronald B. Standler, "Editorial: Mathematics for Engineers," The Journal of Undergraduate Mathematics and Its Applications, Vol. 11, pages 1-6, Spring 1990.

---

Why is mathematics important to engineers? And what in mathematics is most important?

The dialogue about mathematics for engineering students must not be confined just to engineering faculty at four-year universities. Many undergraduate engineering students transfer from two-year colleges, where they took all of their mathematics classes. And all engineering students receive their mathematics "basic training" (in algebra, trigonometry, and analytic geometry) in high school.

I hope in this essay to influence mathematics instructors, particularly those who have little contact with professors of engineering, to consider the needs of their students who will be going on to engineering careers.

Three Key Reasons

There are three keys reasons why mathematics is important for engineers:

1. The laws of nature (e.g., Maxwell's equations for electromagnetics, Kirchhoff's Rules for circuit analysis) are mathematical expressions. Mathematics is the language of physical science and engineering.
2. Mathematics is more than a tool for solving problems; mathematics courses can develop intellectual maturity. It is critical that engineering students learn to visualize abstract concepts.
   
   Many students believe that the way to solve a problem is to search for the proper formula, and then substitute numbers into the formula. This may be all right for solving quadratic equations (except when the factors are obvious), but this is not a good general attitude.
   
   Doing derivations helps the student develop a logical thought process, a discipline of problem solving that is essential for solving engineering problems of many kinds.
   
   Few problems can be solved immediately. It is critical that engineering students develop persistence at solving problems. Often the "best" way does not come instantly or even easily; one must try various methods and see what happens. The experience of working large numbers of homework problems, of diverse kinds, seems to build a personal collection of approaches and tools, and add to an understanding of mathematics.
   
   Many students need more practice in how to start solving a problem, including translating "word problems" into mathematical expressions.
3. Numerical simulation on a digital computer is a powerful and effective tool that is being used by an increasing number of engineers. However, computers do not make traditional mathematical analysis obsolete! The following three reasons support this belief:
   • First, computer programs contain mathematical relations; understanding and fluency with manipulation of these relations is still necessary.
   • Second, debugging computer programs is a difficult art. One of the best ways to validate a program is to compare the computer simulation of simple situations to the analytical solution for the same situation. Knowledge of traditional mathematical analysis is essential for this method of validating computer programs.
   • Third, it is relatively easy to write brute-force computer code that requires a long runtime and produces significant error, owing to accumulation of errors from the limited resolution of machine numbers. Great increases in both speed and accuracy can be obtained by using analytical solutions for parts of the problem, or by careful development of appropriate algorithms. Knowledge of traditional mathematics is highly relevant to this task.

Specific Comments on
Mathematics Courses

The following remarks concern students majoring in engineering. Students majoring in mathematics or computer science would be expected to have different needs. We hope all those needs could be met in common lower-level courses.

Here is a provocative comment, sometimes heard among professor of engineering:

"Proofs of theorems and discussion of axioms, postulates, etc. should receive minor treatment (but not be eliminated!). For example, few successful engineers are able to state Rolle's Theorem in Calculus. Is such material really critical?"

While most engineers do few, if any, proofs, they do many derivations and mathematical operations. Students should receive extensive practice in doing derivations. For example, students should know techniques for expressing sin(a+b) as a function of sin(a), sin(b), cos(a), and cos(b). Engineers usually consult tables of identities for such relations, but learning how to do such derivations is an important intellectual skill. This skill is required in courses on electromagnetic field theory, signal processing, semiconductor physics, etc. We hope that every mathematics examination includes some derivations.

There should be more unknown parameters (e.g., A, B, omega, phi) in problems and exercises, and fewer numerical values. In other words, mathematics courses should be abstract and general.

Extensive treatment of techniques for evaluation of integrals may not be a good use of time. Nearly every engineer or scientist uses tables to evaluate analytical expressions for integrals. But change of variable and integration by parts are essential techniques, even when integral tables are used.

Students need practice in algebraic manipulation to put the solution in a form that is easy to appreciate. It is difficult to state specific criteria for "easy to appreciate," but people who are fluent in mathematics seem to be able to agree that some expressions are "simpler" or more "easy to appreciate" than others. For example, it is important to be able to note easily the asymptotic behavior as the independent variable goes to zero or infinity. It is also important to be able to find the poles and zeros of a function.

Many problems in engineering and applied science involve the solution of either a quadratic equation or a set of N independent linear equations in N variables. Students should be able to solve these equations without difficulty. Some students seem to think that Cramer's rule is the best, or even the only, way to solve a set of linear equations! Gaussian reduction (Gaussian elimination) should also be taught.

The ability to write a differential equation for a particular applied problem should receive little attention in mathematics classes, as that topic is emphasized in engineering and physics classes.

Many professors of engineering and science like the treatment in Calculus and Analytic Geometry by George B. Thomas. While it is inappropriate to demand that this textbook be adopted, we urge that whatever textbook is used have a similar flavor and content.

Fundamental Topics and Goals

There is limited time in high school and the first two years of college to learn all of the mathematics that is important to scientists and engineers. A reasonable goal for engineering students by the end of their sophomore year is to be able to solve the following types of problems.

1. Algebra
   • factor expressions
   • solve N independent linear equations with N variables
   • find roots of any quadratic equation
   • use logarithms to multiply and divide
   • use logarithms to raise any number to any power
   • change of base of logarithms
   • arithmetic and geometric series
   • matrices
   • eigenvector, basis vector
2. Calculus
   • take a derivative of any function
   • integrate functions of one variable (may use tables)
   • find maxima and minima of a function
   • partial derivatives
   • find mean value of any function (moments, centroid)
   • find the derivative of integral whose limits are functions of the variable
3. Analytic Geometry and Calculus
   • trigonometric identities
   • law of cosines, solution of right triangle
   • coordinate systems: rectangular, cylindrical, spherical (and also their two-dimensional counterparts)
   • equation of a straight line: point-slope, slope-intercept, etc.
   • equations for conic sections
   • transformation of coordinates
   • distance between two points, point and line, point and surface
   • find surface area
   • integral of a function over a surface
   • find volume
   • integral of a function in a volume
4. Vector calculus
   • arithmetic with scalars and vectors, unit vectors
   • dot product of two vectors (scalar product)
   • cross product of two vectors (vector product)
   • linear independence or dependence of two vectors
   • divergence and curl operations
   • find tangent and normal vectors (to a curve or surface)
   • how to apply Divergence and Green's theorems
5. Differential equations
   • linear, constant-coefficient, homogeneous, ordinary differential equations of both first and second order.
   • same, but non-homogeneous with an inhomogeneous part that is either:
     A + B t
     A cos(omega t + phi),
     A exp(-t/tau), or
     A exp(-t/tau) cos(omega t + phi).
   • examination of response in both the time and frequency domains
   • resonance and damping (underdamped, critically damped, overdamped)
   • methods of undetermined coefficients and the Laplace transform
6. Complex numbers
   • Argand plane
   • a + ib = c + id   if both   a = c and b = d
   • e^ix = cos(x) + i sin(x)
7. Infinite series
   • how to find Taylor's series expansion (and how and when to use it)
   • Fourier series
   • tests for convergence of series

This is by no means the end of the mathematics that is useful to engineers. Electrical engineers should consider additional courses in:

1. ordinary differential equations,
2. partial differential equations (boundary value problems),
3. functions of a complex variable,
4. statistics, and
5. numerical analysis (particularly: root finding, integration, evaluation of transcendental functions, fitting equations to empirical data, numerical solution of differential equations).

I doubt that many traditionally educated mathematicians will balk at any of the above. In an era, however, when the content of the core mathematics courses of the first two years of college is up for free discussion, engineering faculty feel it is important that the needs of the engineering curriculum be heard.

Ronald B. Standler

---

This document is at   http://www.rbs0.com/math.htm
posted on the Internet 13 May 2000

Return to my personal homepage.

_____________________________________________________________________________

http://www.etymonline.com/zero.php






History of Zero
Historical scientists categorize the types of number systems peoples use, much the same way philologists break down languages into "analytic," "agglutinative," "inflectional," etc.
The path that leads to the discovery of "0" lies only in the most advanced type of number system, which is called "positional" because the value of a character depends on its position. Our modern way of counting is positional. The base figure "5" has a different value in 514 and in 145, determined by its position.
The Romans, Greeks, Hebrews (and Aztecs and pre-Islamic Arabs and a great many others) used an "additive" system, which is fundamentally a transcription of counting. A Roman "V" meant "five" and that's all it could mean.
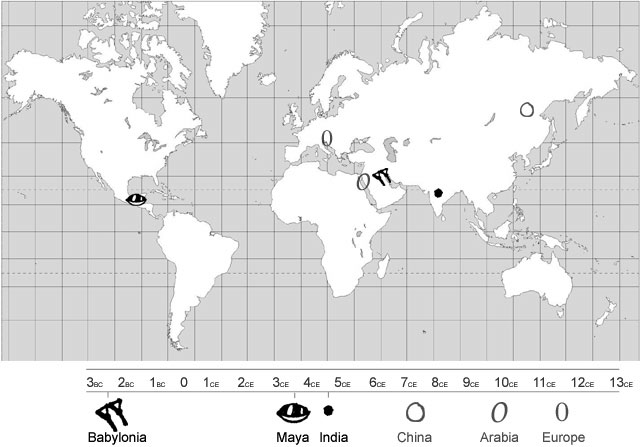
An additive system can develop into a positional one -- the abacus has a tendency to suggest the positional model -- but as far as we know, the positional concept has emerged in only four places: c.2000 B.C.E., in Babylon; around the start of the Common Era, in China; between the 4th and 9th centuries C.E. among the Mayan astronomer-priests; and in India.
Positional systems have certain features in common. One is that each base number is denoted by a discrete symbol, purely conventional and not a graphic representation of the number itself (i.e., not "four slashes" for "four," as the Greeks and Romans had). Imagine the scribal confusion if the Romans had tried to use positional mathematics with their numbering system: "423" would be IIII II III, while "342" would be III IIII II.
Another feature of positional number systems is that they lack special symbols for numbers which are orders of magnitude of the base number. Romans had a symbol for "10," and a separate symbol for "100" (10 x 10) and another for "1,000" (10 x 100) and so on. This is necessary in an additive system, for simplicity of notation and record-keeping, but it is incompatible with a positional system.
But think about the positional system. You come across a big stumbling block when you try to write a number like 2,002. For a Roman, that's no problem: MMII. But in a positional system, you have to find a way to indicate the absence of "tens" and "hundreds." You could leave a gap (the Babylonians did this at first), but that opens the door to more scribal errors, and anyway how do you indicate two gaps, as in 2,002?
It becomes necessary to have a "zero," a character that signifies "empty." Maybe not necessary, because the brilliant Chinese mathematicians somehow managed to run a positional system without making this discovery. The Babylonians (eventually), the Indians, and the Mayans did discover it, however.
But the next step, the true miracle moment, is to realize that that "symbol for nothing" that you're using is not just a place-holder, but an actual number: that "empty" and "nothing" are one. The null number is as real as "5" and "2,002" -- that's when the door blows open and the light blazes forth and numbers come alive. Without that, there's no modern mathematics, no algebra, no modern science.
And as far as we know, that has only happened once in human history, somewhere in India, in the intellectual flowering under the Gupta Dynasty, about the 6th century C.E. There was no "miracle moment," of course. It was a long, slow process.
The daunting realization, for heirs of "Western Civilization," is that the Greek and Roman cultures we revere were benighted mathematically, plodding along in the most primitive of number systems. But as champions of these cultures point out, we can admire their accomplishments all the more for that.
Some authorities, however, put up strong resistance to the theory of the Indian origin of modern mathematics. At first, they were mired in the same religion-based worldview that denied the Indo-European linguistic link: the number system simply had to be Hebrew in origin, because nothing else would comport with the Bible (so they thought). Later, however, resistance took refuge in unwillingness to concede cultural superiority to non-Western civilizations.
It does seem to be a glaring omission in the "Greek miracle." Historical scientists in the early part of the 20th century (such as G.R. Kaye, N. Bubnov, B. Carra de Vaux, etc.) argued strongly against an Indian origin, insisting the numbers evolved in ancient Greece, perhaps among neo-Pythagoreans, were taken to Alexandria, and from there spread to Rome and Spain in the west (from whence medieval Europe rediscovered them), and, via trade routes, to India in the east.
Among the many problems with this idea is the utter lack of documentary evidence for anything like a positional number system in Greece or Rome, and its requirement that we believe ancient people had made this wonderful practical discovery, yet did not put it to any use.
Speculation about a Greek origin of the ten "Arabic numerals" goes back to the 16th century in Europe. But before that, there are many sources in Europe and the pre-Islamic Levant that frankly attribute them to India. The earliest depiction of them in English, "The Crafte of Nombrynge" (c.1350), correctly identifies them as "teen figurys of Inde."
The Arabic sources, from the earliest times, refer to them as arqam al hind -- "figures from India" -- or some such name. The Muslims of that day, generally contemptuous of non-Islamic culture, had no problem conceding the invention of this number system to India.

« A Half Diet | Main | Stupid speaking »

January 10, 2004

A BRIEF HISTORY OF ZERO

A BRIEF HISTORY OF ZERO

Kristen McQuillin, July 1997 (revised January 2004)

Once upon a time there was no zero. Of course people knew if they had nothing, but there was no mathematical notation for it. Zero was independently invented only three times.
The first recorded zero is attributed to the Babylonians in the 3rd century BC. A long period followed when no one else used a zero place holder. But then the Mayans, halfway around the world in Central America, independently invented zero in the fourth century CE. The final independent invention of zero in India was long debated by scholars, but seems to be set around the middle of the fifth century. It spread to Cambodia around the end of the 7th century. From India it moved into China and then to the Islamic countries. Zero finally reached western Europe in the 12th century.
Before you continue reading the history of zero, please be sure you understand theseunderlying concepts : Number vs Numeral; Invent vs Discover & Place Value Notation

BABYLONIA: 300 B.C.

The Babylonians were the first culture to invent the place value system. They had a sexigesimal number system, that is, they counted in 60s, as we count in tens. When you count minutes in an hour or measure circles you are thinking in sexigesimal.
Of course the Babylonians didn’t use our numerals. They wrote in cuneiform, a writing system optimized for writing in damp clay tablets. The