REf
http://simplestcodings.blogspot.in/2013/09/graphs.html
http://simplestcodings.blogspot.in/2013/09/graphs.html
http://sun.iwu.edu/~sander/CS255/Notes/AdjLists.html
http://www.sanfoundry.com/cpp-program-describes-graph-representation-using-adjacency-list/
http://iamsoftwareengineer.blogspot.in/2012/06/c-graph-implementation-with-adjacency.html
http://stackoverflow.com/questions/11547875/graph-adjacency-list-representation
http://www.geeksforgeeks.org/graph-and-its-representations/

#include <stdio.h>
#include <stdlib.h>

struct graphnode
{
int name;
struct graphnode *next;
};

void addNode(struct graphnode *G[],int startNode, int endNode)
{
// creating a new linked list which is to be added
struct graphnode *tmp;
tmp->name=endNode;
tmp->next=G[startNode];
startNode=tmp;
}

void printGraph(struct graphnode *G[], int numofnodes)
{
int i;
for(i=0;i<numofnodes;i++)
{
    struct graphnode *tmp;
    tmp=G[i];
    printf("%d",i);

    while(tmp!=NULL)
    {
        printf("%d",tmp->name);
        tmp=tmp->next;
    }
}
}

int main(void)
{
int numofnodes;
printf("Enter the number of nodes: ");
scanf("%d",&numofnodes);

// Note that we have created depending upon the size inputted by the user
struct graphnode *arrayOfVertices[numofnodes];
int i;      // for iteration

for(i=0;i<numofnodes;i++)
{
    arrayOfVertices[i]->name=i;
    arrayOfVertices[i]->next=NULL;
}

addNode(arrayOfVertices,0,1);
addNode(aarrayOfVertices,0,2);
printGraph(arrayOfVertices,numofnodes);

return 0;
}

C Graph implementation with adjacency list representation using structures: Data Structure Tutorial 1

This is a quick tutorial for implementing graph data structure with adjacency list representation. Once I was
looking on the web to have a simple introductory tutorial on graphs, but unfortunately couldn’t find one
simple enough. So I decided to write this.

In the adjacency list representation,

è All the vertices are stored in an array of structure containing ‘data’ and ‘link’ fields.

è The linked chains represent the edges of a vertex with its neighbors.

In the figure, there are 6 vertices, represented by the array of length 6, and the chains represent the edges.

Below is another example:

Let us first define the structure of a vertex in a graph.

struct vertex

{

int vertexKey;

struct edge *edgePtr;

}vertex;

The vertexKey is the data field of the vertex, and edgePtr is the edge pointer, declared next.

The graph can be declared as:

struct vertex graph[10];

int vertexCount=0;

Here, we are taking the maximum number of vertices as 10.

The vertexCount gives us the number of vertices in the graph at a time.

Now, let us define the structure of an edge:

struct edge
{

int vertexIndex;

struct edge *edgePtr;

}edge;

Here, the vertexIndex field stores the index of the vertex to which the original vertex in the
array is connected.

The following figure should make the structures clear:

Inserting new vertex:

We have to insert a new vertex without any edges.

This can be implemented by incrementing the vertexCount and storing the vertex data in the
graph array at vertexCount position.

void InsertVertex(int vertexKey)

{

graph[vertexCount].vertexKey=vertexKey;

graph[vertexCount].edgePtr=NULL;

vertexCount++;

}

Note that the edgePtr of the newly inserted vertex should point to NULL, i.e., it is a null
pointer.

Now lets move on to insertion of an edge. The function is given below:

void insertEdge(int vertex1, int vertex2)

{

struct edge *e,*e1,*e2;

//For first vertex

e=graph[vertex1].edgePtr;

while(e&& e->edgePtr)

{

e=e->edgePtr;

}

e1=(struct edge *)malloc(sizeof(*e1));

e1->vertexIndex=vertex2;

e1->edgePtr=NULL;

if(e)

e->edgePtr=e1;

else

graph[vertex1].edgePtr=e1;

//For second vertex

e=graph[vertex2].edgePtr;

while(e&& e->edgePtr)

{

e=e->edgePtr;

}

e2=(struct edge *)malloc(sizeof(*e2));

e2->vertexIndex=vertex1;

e2->edgePtr=NULL;

if(e)

e->edgePtr=e2;

else

graph[vertex2].edgePtr=e2;

}

For inserting an edge, we just move to the end of the linked list of the corresponding vertex,
and insert new edge there. We have to do this for both the vertices.

And finally, here is the implementation for printing the graph:

void printGraph()

{

int i;

struct edge *e;

for(i=0;i<vertexCount;i++)

{

printf("%d(%d)",i,graph[i].vertexKey);

e=graph[i].edgePtr;

while(e)

{

printf("->%d",e->vertexIndex);

e=e->edgePtr;

}

printf("\n");

}

To summarize, the full code is given below:

#include<stdio.h>

#include<stdlib.h>

struct edge

{

int vertexIndex;

struct edge *edgePtr;

}edge;

struct vertex

{

int vertexKey;

struct edge *edgePtr;

}vertex;

struct vertex graph[10];

int vertexCount=0;

void InsertVertex(int vertexKey)

{

graph[vertexCount].vertexKey=vertexKey;

graph[vertexCount].edgePtr=NULL;

vertexCount++;

}

void insertEdge(int vertex1, int vertex2)

{

struct edge *e,*e1,*e2;

e=graph[vertex1].edgePtr;

while(e&& e->edgePtr)

{

e=e->edgePtr;

}

e1=(struct edge *)malloc(sizeof(*e1));

e1->vertexIndex=vertex2;

e1->edgePtr=NULL;

if(e)

e->edgePtr=e1;

else

graph[vertex1].edgePtr=e1;

e=graph[vertex2].edgePtr;

while(e&& e->edgePtr)

{

e=e->edgePtr;

}

e2=(struct edge *)malloc(sizeof(*e2));

e2->vertexIndex=vertex1;

e2->edgePtr=NULL;

if(e)

e->edgePtr=e2;

else

graph[vertex2].edgePtr=e2;

}

void printGraph()

{

int i;

struct edge *e;

for(i=0;i<vertexCount;i++)

{

printf("%d(%d)",i,graph[i].vertexKey);

e=graph[i].edgePtr;

while(e)

{

printf("->%d",e->vertexIndex);

e=e->edgePtr;

}

printf("\n");

}

main()

{

InsertVertex(5);

InsertVertex(3);

InsertVertex(4);

InsertVertex(2);

InsertVertex(9);

insertEdge(0,1);

insertEdge(0,2);

insertEdge(1,3);

insertEdge(1,4);

printGraph();

return 0;

}

The ‘main’ function is for testing of the following graph:

And the final output is:

The data for each vertex is written in the braces.

Now, this implementation of graph is useful for almost all applications, but is not optimum for
‘delete vertex’ operation. For this, we will have to use a linked list instead of an array for
storing the vertices. This is shown below:

That completes our first tutorial on graphs. In the next tutorial, we will discuss graph
operations like ‘depth-first-search’, ‘breadh-first-search’ etc.

If you have any queries or doubts, please ask through comments.

If you like this post, please consider to buy me a coffee.

Don’t forget to subscribe this blog through email.

Posted 23rd June 2012 by sWebDev

View comments

അഖില്‍June 20, 2013 at 2:36 AM

I would like to read second part of graph tutorial(DFS,BFS).
Where I can find it?
Reply
Replies
brylle cabanalJuly 7, 2013 at 3:12 AM

Thank you sir. Sir can you help me to code the adjacency list with an input file? I hope you can help me sir. I am a 1st year computer science.
Reply
Replies
sidharthJuly 25, 2013 at 6:21 AM

suppose i have 2d file
first collumn of file represent vertex of graph
n all the elements of row(except 1st )represents the edges of vertex (1st element of that row)
so how will i use this file in above code???
its very difficlut to put all the edge like u did...
can u post the code in c.
Reply
Replies

In 1997, making a website seemed like the simplest thing in the world. Of course, it wasn't — there was all sorts of HTML code involved, and making a professional-looking site took almost as much work then as it does now.

Facebook Inc (FB.O) is paying $55 million to $60 million to buy Face.com, according to people familiar with the matter, acquiring the company that provides the facial-recognition technology used by the world's largest social network to help users identify and tag photos.

Google wants love. But so do six other companies. They are after .love, actually, a new "top-level domain" that could catch on as .com, .org and .net did.

Love might not prevail, but chances are, at least one of the domains in 1,930 applications for new extensions will.

Given a Directed Graph and two vertices in it, check whether there is a path from the first given vertex to second. For example, in the following graph, there is a path from vertex 1 to 3. As another example, there is no path from 3 to 0.

Researchers have developed a new software that can easily transformgrayscale images into stunning yet realisticcolours, utilising the vast amount of imagery available on the internet.

Problem Statement:

The Government of Byteland has decide to issue new currency notes with special protection features to commemorate a great mathematician.

In a party of N people, only one person is known to everyone. Such a person may be present in the party, if yes, (s)he doesn’t know anyone in the party. We can only ask questions like “does A know B? “. Find the stranger (celebrity) in minimum number of questions.

WhereChandigarh

OrganizerCompareall(Start-up)

Important Dates

Start Date: June 10, 2012

End Date : June 5, 2012

Deadline: June 30, 2012

Eligibility Undergrad Level

Type of Opportunity Internship/Training

Published OnJune 5, 2012

Need a website developer for start up by IITian.

WhereMumbai

OrganizeriLogo(Start-up)

Important Dates

Start Date: June 1, 2012

Deadline: June 11, 2012

Eligibility Undergrad Level,Grad Level,Postgrad Level,Non-students

Type of Opportunity Internship/Training

Tags Technology, Software Engg./Coding/Programming

Published OnMay 30, 2012

Abou

Dynamic Views template. Powered by Blogger.

Graph Implementation in C

A graph is a collection of nodes and edges. These nodes are connected by links(edges).
These edges may be directed or undirected. Moreover these edges can have weights associated with them

So edges can be categorized as :

Directed, weighted edges
Directed, unweighted edges
Undirected, weighted edges
Undirected, unweighted edges

Uses of graphs

Graphs are extremely useful. Look everywhere and one can easily find use of graphs. Listed below are a few of the vast set of practical uses of graphs.

Delhi Metro Rail Map

Each station is a vertex, the distance in between is a weighted edge.

A Maze

Each corner is a vertex, Line between two corners is and edge.

A tournament fixture
Courtesy: http://www.squadtd.com/

Each team is a vertex, match between the teams is an edge.

Kind of graphs

There are numerous classifications and types of graphs available. I have collected a few of those types from various sources and organized a list of types of graphs:

Undirected Graphs

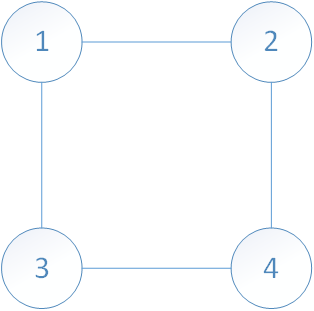Undirected Graph

Characteristics:

Order of vertices doesn't matter
1-2 is same as 2-1

Directed Graphs

Directed Graph

Characteristics:

Order of vertices does matter
1-2 is not same as 2-1

Vertex labeled Graphs.

Vertex Labeled Graph

Characteristics:

Each vertex contains additional information. e.g {2,orange}, {4,green}

Cyclic Graphs.

Cyclic Graph

Characteristics:

Graph contains at least one cycle.

Edge labeled Graphs.

Edge Labeled Graph

Characteristics:

Edge has labels e.g an edge in the above graph will be represented as {orange,green,{blue,cyan}}

Weighted Graphs.

Weighted Graph

Characteristics:

Each edge has some weight associated with it.

Directed Acyclic Graphs.

Direct Acyclic Graph(DAG)

Characteristics:

Graph has no cycles.

Disconnected Graphs

Disconnected Graph

Characteristics:

Vertices are disconnected

Mixed graph

Mixed Graph

Characteristics:

Some edges may be directed and some may be undirected

Multigraph

Characteristics:

Multiple edges (and sometimes loops) are allowed

Quiver

Characteristics:

Directed graph which may have more than one arrow from a given source to a given target. A quiver may also have directed loops in it.

Representation of graphs:

Fig. 1: An undirected graph

Fig 2: A directed graph

In order to use Graphs programatically , they need to be somehow represented in code. Following are the most widely used methods of representing a graph.

Adjacency Matrix :

For N vertices an adjacency matrix is an NxN array A such that
A[i][j] = 1 if there is an edge E(i,j)
= 0 otherwise

For an undirected graph, A[i][j] = A[j][i]

For weighted graphs,
A[i][j] = weight of the edge, if there is an edge E(i,j)
= a constant representing no edge (e.g a very large or very small value)

For Fig 1, the adjacency matrix would be

The adjacency matrix for directed graph in Fig 2 would be:

Adjacency List :

Adjacency matrix representation consume a lot of memory (O[N²]). If the graph is complete or almost complete(i.e. contains most of the edges between the vertices), then this representation is good to use. But if there are very few edges as compared to number of vertices, it will unnecessarily consume extra space. Adjacency list can handle this situation very optimally.

Every vertex has a linked list of the vertices it is connected with.

Adjacency list for Fig 1 would be:

Adjacency list for Fig 2 would be:

Following is code snippet to implement graphs in C using adjacency list.

/*graph.h*/

#ifndef _GRAPH_H_

#define _GRAPH_H_

typedef enum {UNDIRECTED=0,DIRECTED} graph_type_e;

/* Adjacency list node*/

typedef struct adjlist_node

{

    int vertex;                /*Index to adjacency list array*/

    struct adjlist_node *next; /*Pointer to the next node*/

}adjlist_node_t, *adjlist_node_p;

/* Adjacency list */

typedef struct adjlist

{

    int num_members;           /*number of members in the list (for future use)*/

    adjlist_node_t *head;      /*head of the adjacency linked list*/

}adjlist_t, *adjlist_p;

/* Graph structure. A graph is an array of adjacency lists.

   Size of array will be number of vertices in graph*/

typedef struct graph

{

    graph_type_e type;        /*Directed or undirected graph */

    int num_vertices;         /*Number of vertices*/

    adjlist_p adjListArr;     /*Adjacency lists' array*/

}graph_t, *graph_p;

/* Exit function to handle fatal errors*/

inline void err_exit(char* msg)

{

    printf("[Fatal Error]: %s \nExiting...\n", msg);

    exit(1);

}

#endif

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

120

121

122

123

124

125

126

127

128

129

130

131

132

133

134

135

/*graph.c*/

#include <stdio.h>

#include <stdlib.h>

#include "graph.h"

/* Function to create an adjacency list node*/

adjlist_node_p createNode(int v)

{

    adjlist_node_p newNode = (adjlist_node_p)malloc(sizeof(adjlist_node_t));

    if(!newNode)

        err_exit("Unable to allocate memory for new node");

    newNode->vertex = v;

    newNode->next = NULL;

    return newNode;

}

/* Function to create a graph with n vertices; Creates both directed and undirected graphs*/

graph_p createGraph(int n, graph_type_e type)

{

    int i;

    graph_p graph = (graph_p)malloc(sizeof(graph_t));

    if(!graph)

        err_exit("Unable to allocate memory for graph");

    graph->num_vertices = n;

    graph->type = type;

    /* Create an array of adjacency lists*/

    graph->adjListArr = (adjlist_p)malloc(n * sizeof(adjlist_t));

    if(!graph->adjListArr)

        err_exit("Unable to allocate memory for adjacency list array");

    for(i = 0; i < n; i++)

    {

        graph->adjListArr[i].head = NULL;

        graph->adjListArr[i].num_members = 0;

    }

    return graph;

}

/*Destroys the graph*/

void destroyGraph(graph_p graph)

{

    if(graph)

    {

        if(graph->adjListArr)

        {

            int v;

            /*Free up the nodes*/

            for (v = 0; v < graph->num_vertices; v++)

            {

                adjlist_node_p adjListPtr = graph->adjListArr[v].head;

                while (adjListPtr)

                {

                    adjlist_node_p tmp = adjListPtr;

                    adjListPtr = adjListPtr->next;

                    free(tmp);

                }

            }

            /*Free the adjacency list array*/

            free(graph->adjListArr);

        }

        /*Free the graph*/

        free(graph);

    }

}

/* Adds an edge to a graph*/

void addEdge(graph_t *graph, int src, int dest)

{

    /* Add an edge from src to dst in the adjacency list*/

    adjlist_node_p newNode = createNode(dest);

    newNode->next = graph->adjListArr[src].head;

    graph->adjListArr[src].head = newNode;

    graph->adjListArr[src].num_members++;

    if(graph->type == UNDIRECTED)

    {

        /* Add an edge from dest to src also*/

        newNode = createNode(src);

        newNode->next = graph->adjListArr[dest].head;

        graph->adjListArr[dest].head = newNode;

        graph->adjListArr[dest].num_members++;

    }

}

/* Function to print the adjacency list of graph*/

void displayGraph(graph_p graph)

{

    int i;

    for (i = 0; i < graph->num_vertices; i++)

    {

        adjlist_node_p adjListPtr = graph->adjListArr[i].head;

        printf("\n%d: ", i);

        while (adjListPtr)

        {

            printf("%d->", adjListPtr->vertex);

            adjListPtr = adjListPtr->next;

        }

        printf("NULL\n");

    }

}

int main()

{

    graph_p undir_graph = createGraph(5, UNDIRECTED);

    graph_p dir_graph = createGraph(5, DIRECTED);

    addEdge(undir_graph, 0, 1);

    addEdge(undir_graph, 0, 4);

    addEdge(undir_graph, 1, 2);

    addEdge(undir_graph, 1, 3);

    addEdge(undir_graph, 1, 4);

    addEdge(undir_graph, 2, 3);

    addEdge(undir_graph, 3, 4);

    addEdge(dir_graph, 0, 1);

    addEdge(dir_graph, 0, 4);

    addEdge(dir_graph, 1, 2);

    addEdge(dir_graph, 1, 3);

    addEdge(dir_graph, 1, 4);

    addEdge(dir_graph, 2, 3);

    addEdge(dir_graph, 3, 4);

    printf("\nUNDIRECTED GRAPH");

    displayGraph(undir_graph);

    destroyGraph(undir_graph);

    printf("\nDIRECTED GRAPH");

    displayGraph(dir_graph);

    destroyGraph(dir_graph);

    return 0;

}

Sources:
http://en.wikipedia.org/wiki/Graph_(mathematics)
http://web.cecs.pdx.edu/~sheard/course/Cs163/Doc/Graphs.html
http://msdn.microsoft.com/en-us/library/ms379574(v=vs.80).aspx

Posted 29th September 2013 by Varun Gupta

Labels: BFS DAG DFS Graphs Quiver

Builder Design Pattern Implementation in C++

Sometimes an application gets too complicated and developing it becomes a pain. These applications contain complex objects which are made up from other objects from different classes. Now these objects may vary. So there has to be a process of building the complex objects so that there is scope of building different products using the same process.

That is when a creational design pattern called Builder comes into picture. It separates the details of construction process from its representation.

Now what in the world that line means actually ?

It means that the construction process is made so generic, that multiple products can be produced using the same process. e.g. construction workers. Different type of buildings can be built using the same workers and same common set of process.

Here is a class diagram of the design pattern.

Builder Design Pattern

There are 4 major components:

Director: It constructs an object using the Builder interface.
Builder : It specifies an abstract interface to build parts of a product.
Concrete Classes : Implements builder interface.
Product : The complex object which is created at the end.

Director object is created and Builder interface is used. It notifies the Builder to create each part of the product. Upon the request from Director, Builder adds parts to the product. Finally the product is returned by the Builder.

We have to take care of when to use the Builder Design Pattern. Few points come into mind :

When the object to be created is complex enough and can have multiple representations.
When the construction process can be broken down into multiple steps
When the process of creation of an object can be independent of the parts to be used.
When different products can have a common abstract class.

Now lets create a builder design pattern using an example.

Builder Example

In this example we create house as product. Now the house created may be different as per requirement of different people. It can be a lavish house with lots of amenities and expensive stuff. On the other hand, it could be a normal house with normal stuff.

The HouseBuilder class is the builder class which provides interface for creating the parts of the house.
The House class is the final product that we want to build
LavishHouse and NormalHouse are the concrete classes which implement the HouseBuilder interface.
Contractor is the director which constructs the house using the HouseBuilder interface.

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

120

121

122

123

124

125

126

127

128

129

130

131

132

133

134

135

136

137

138

139

140

141

142

143

144

145

146

147

148

149

150

151

152

153

154

155

156

157

158

159

160

161

162

163

164

165

166

167

168

169

170

171

172

173

174

175

176

177

178

179

180

181

182

183

184

185

186

#include <iostream>

using namespace std;

/* Interface that will be returned as the product from builder */

class HousePlan{

public:

 virtual void setWindow(string window)=0;

 virtual void setDoor(string door)=0;

 virtual void setBathroom(string bathroom)=0;

 virtual void setKitchen(string kitchen)=0;

 virtual void setFloor(string floor)=0;

};

/* Concrete class for the HousePlan interface */

class House:public HousePlan{

private :

 string window, door, kitchen, bathroom, floor;

public:

 void setWindow(string window)

 {

  this->window = window;

 }

 void setDoor(string door)

 {

  this->door = door;

 }

 void setBathroom(string bathroom)

 {

  this->bathroom = bathroom;

 }

 void setKitchen(string kitchen)

 {

  this->kitchen = kitchen;

 }

 void setFloor(string floor)

 {

  this->floor = floor;

 }

};

/* Builder Class */

class HouseBuilder

{

public:

 /* Abstract functions to build parts */

 virtual void buildWindow()=0;

 virtual void buildDoor()=0;

 virtual void buildKitchen()=0;

 virtual void buildBathroom()=0;

 virtual void buildFloor()=0;

 /* The product is returned by this function */

 virtual House* getHouse()=0;

};

/* Concrete class for the builder interface */

class LavishHouse:public HouseBuilder{

private:

 House *house;

public:

 LavishHouse()

 {

  house = new House();

 }

 void buildWindow()

 {

  house->setWindow("French Window");

 }

 void buildDoor()

 {

  house->setDoor("Wooden Door");

 }

 void buildBathroom()

 {

  house->setBathroom("Modern Bathroom");

 }

 void buildKitchen()

 {

  house->setKitchen("Modular Kitchen");

 }

 void buildFloor()

 {

  house->setFloor("Wooden Floor");

 }

 House* getHouse()

 {

  return this->house;

 }

};

/* Another Concrete class for the builder interface */

class NormalHouse:public HouseBuilder{

private:

 House *house;

public:

 NormalHouse()

 {

  house = new House();

 }

 void buildWindow()

 {

  house->setWindow("Normal Window");

 }

 void buildDoor()

 {

  house->setDoor("Metal Door");

 }

 void buildBathroom()

 {

  house->setBathroom("Regular Bathroom");

 }

 void buildKitchen()

 {

  house->setKitchen("Regular Kitchen");

 }

 void buildFloor()

 {

  house->setFloor("Mosaic Floor");

 }

 House* getHouse()

 {

  return this->house;

 }

};

/* The Director. Constructs the house */

class Contractor

{

private:

 HouseBuilder *houseBuilder;

public:

 Contractor(HouseBuilder *houseBuilder)

 {

  this->houseBuilder = houseBuilder;

 }

 House *getHouse()

 {

  return houseBuilder->getHouse();

 }

 void buildHouse()

 {

  houseBuilder->buildWindow();

  houseBuilder->buildDoor();

  houseBuilder->buildBathroom();

  houseBuilder->buildKitchen();

  houseBuilder->buildFloor();

 }

};

/* Example on how to use the Builder design pattern */

int main()

{

 HouseBuilder *lavishHouseBldr = new LavishHouse();

 HouseBuilder *normalHouseBldr = new NormalHouse();

 Contractor *ctr1 = new Contractor(lavishHouseBldr);

 Contractor *ctr2 = new Contractor(normalHouseBldr);

 ctr1->buildHouse();

 House *house1 = ctr1->getHouse();

 cout<<"Constructed: "<<house1;

 ctr2->buildHouse();

 House *house2 = ctr2->getHouse();

 cout<<"Constructed: "<<house2;

}

Posted 2nd April by Varun Gupta

Labels: Builder Builder Design Pattern Design Patterns

c program

C program for dfs (depth first search)

June 26, 2013 Akshay upadhyay 1 Comment

c program for dfs(depth first search) using array. DFS is Depht first Search, which is used to traverse un-weighted Graph. There are two most popular graph traversing technique, i.e DFS and BFS. DFs make use of Stack while, BFS make use data structure Queue. Also see c program for bfs.

C program for dfs

#include<stdio.h>
#include<conio.h>

char stack[20];
int top=-1, n;
char arr[20];
char dfs(int );
char ajMat[20][20];
char b[20];
void display();
int p=0;

int main()
{
    char v;
    int l=0;
    printf("Enter the number of nodes in a graph");
    scanf("%d",&n);
    printf("Enter the value of node of graph");
    for(int i=0; i<n; i++)
    {
        scanf("%s",&b[i]);
    }
    char k=b[0];
    printf("Enter the value in adjancency matrix in from of 'Y' or 'N'\n");
    printf("\nIf there is an edge between the two vertices then enter 'Y' or 'N'\n");
    for(int i=0; i<n; i++)
    printf(" %c ",b[i]);
    for(int i=0;i<n; i++)
    {
         printf("\n%c ",b[i]);
         for(int j=0; j<n; j++)
         {
              printf("%c ",v=getch());
              ajMat[i][j]=v;
         }
         printf("\n\n");
    }
    for(int i=0;i<n;i++)
    {
         l=0;
         while(k!=b[l])
         l++;
         k=dfs(l);
    }
    display();
    getch();
}

void display()
{
     printf(" DFS of Graph : ");
     for(int i=0; i<n; i++)
     printf("%c ",arr[i]);
}
void push(char val)
{
     top=top+1;
     stack[top]=val;
}
char pop()
{
     return stack[top];
}

bool unVisit(char val)
{
      for(int i=0; i<p; i++)
      if(val==arr[i])
      return false;
      for(int i=0; i<=top; i++)
      if(val==stack[top])
      return false;
      return true;
}

char dfs(int i)
{
     int k;
     char m;
     if(top==-1)
     {
          push(b[i]);
     }
     m=pop();
     top--;
     arr[p]=m;
     p++;
     for(int j=0; j<n; j++)
     {
          if(ajMat[i][j]=='y')
          {
               if(unVisit(b[j]))
               {
                     push(b[j]);
               }
          }
     }
    return stack[top];
}

Here is the Graph for below output :

Output of C program for dfs:

One thought on “C program for dfs (depth first search)”

rakesh

November 5, 2013 at 9:30 pm

i need to find tree edges and back edges program.would you help me..?

Reply

Code Coding

http://www.geeksforgeeks.org/graph-and-its-representations/

http://enggedu.com/lab_exercise/data_structure_lab/C_program_to_implement_graph_traverses_using_depth_first_search.php

http://www.cs.yale.edu/homes/aspnes/pinewiki/C%282f%29Graphs.html

http://www.coders-hub.com/2013/04/bfs-and-dfs-program-in-c.html#.VB8yjldxgtw

http://www.cprogramto.com/c-program-for-dfs-depth-first-search/

http://www.help2engg.com/program/dfs-programs

http://keviv03.blogspot.in/2012/05/to-implement-graph-using-adjacency-list.html

http://www.thelearningpoint.net/computer-science/algorithms-graph-traversal--depth-first-search--with-c-program-source-code

https://www.google.co.in/search?biw=1138&bih=526&q=breadth+first+search+program+in+c&revid=1534365621&sa=X&ei=pS8fVMOvNIvluQSfg4LoBQ&sqi=2&ved=0CH8Q1QIoBA

https://www.google.co.in/search?biw=1138&bih=526&q=dfs+program+in+c+with+output&revid=1534365621&sa=X&ei=pS8fVMOvNIvluQSfg4LoBQ&sqi=2&ved=0CIEBENUCKAY

Sunday, September 21, 2014

View comments

Uses of graphs

Kind of graphs

Undirected Graphs

Directed Graphs

Vertex labeled Graphs.

Cyclic Graphs.

Edge labeled Graphs.

Weighted Graphs.

Directed Acyclic Graphs.

Disconnected Graphs

Mixed graph

Multigraph

Quiver

Representation of graphs:

Adjacency Matrix :

Adjacency List :

C program for dfs

Output of C program for dfs:

One thought on “C program for dfs (depth first search)”

Leave a Reply

Code Coding

My Blog List